Spiegazione con supporto fisico (II° livello)

In questa fase dell'unità didattica sono ripresi alcuni punti già incontrati durante il Racconto per darne una chiave di lettura più approfondita; queste precisazioni possono riguardare l'analisi di alcune formule, il calcolo di alcuni ordini di grandezza, le considerazioni sulla struttura del reattore ed altre osservazioni che nel discorso precedente si sono rese necessarie. 

Le leggi fisiche, anche espresse in formule, saranno per lo più commentate, non si richiede la loro utilizzazione o la capacità di ricostruirle.

Massa ed energia

Nella trattazione della fisica nucleare si incontra spesso la formula  E = mc² : secondo essa ogni massa per quanto piccola possiede un’enorme quantità di energia. Calcoliamo quanta massa-energia ‘teorica’ contiene la massa di un chilogrammo di una data sostanza; si tratta di circa 3´10¹⁰ kWh, una quantità vicina alla metà dell’energia consumata giornalmente negli USA!

Allora si può proporre agli studenti di riflettere sul fatto che protoni e neutroni non si possono distruggere, ma si può produrre energia riordinandoli in forme che hanno massa totale diversa Þ la fissione.

A questo punto l’insegnante può introdurre la differenza tra la legge di conservazione delle particelle pesanti (il cui numero resta costante) e quelle leggere, aprendo una porta opzionale su un po’ di fisica delle particelle.

Può essere interessante calcolare quanta energia si libera nella fissione di 1 kg di ²³⁵U : dai calcoli si trovano 200 MeV per nucleo (1 eV = 1,6 ´ 10^-19 J)e poiché ci sono 2,5´10 ²⁴ atomi, in totale l’energia liberata è 8´10 ²⁰ erg. I numeri sono ovviamente arrotondati, ma il numero, anche in Joule, è comunque rilevante e bisogna usarlo per ‘stupire’ gli studenti, altrimenti non si rendono conto dell’energia con la quale stanno giocando: si può dire loro che questa è l’energia per esempio necessaria ad innalzare la temperatura di 44 milioni di litri d’acqua dalla temperatura  ambiente al punto di ebollizione!

Bisogna poi sottolineare che i 200 MeV di cui sopra sono solo lo 0,1% della massa-energia iniziale del nucleo di uranio, perché a causa dell’elevato numero atomico, il 99,9% della massa rimane nei neutroni e protoni. Allora è opportuno ricordare anche alla classe per i dovuti confronti che per es. il carbone durante una combustione chimica, converte in energia spendibile solo il 10^-10 circa della massa-energia, poiché l’energia immagazzinata dalle molecole sotto forma di energia di legame è piuttosto piccola; quindi il rendimento di combustibili fissionabili è circa 10⁷ volte migliore di quelli tradizionali.

Per un quadro più generale è possibile analizzare una tabella di questo tipo o simile, purché permetta una riflessione sulle diverse capacità della sostanze nel fornire energia.

Energia ottenibile da 1 kg di materia (misurata dal tempo per cui, con l’energia generata, rimarrebbe accesa una lampadina da 100 W)

Ovviamente non tutti i processi indicati sono attualmente realizzabili con la tecnologia a disposizione, ma seppure limiti teorici, questi esempi servono sempre per prendere coscienza dell’entità del fenomeno.

Se si confrontano i 680 anni della fissione con i 5 s del lavoro meccanico, si sarebbe portati a concludere che: 680 anni = 680 ´ 365 ´ 24 ´ 3600 s  rappresentano un investimento migliore di circa 10⁹ volte nella produzione di energia, ma attenzione alle quantità disponibili di materiale ed alla rinnovabilità delle fonti!! Vogliamo confrontare i kg di U con quelli d’acqua presenti sulla Terra?

I  neutroni  termici

Penso sia il caso di analizzare come funzionano questi efficaci, ma inaspettati, proiettili, iniziando dal fatto che ‘termico’ non vuol dire ‘riscaldato’, ma a temperatura ambiente: cioè al neutrone attribuiamo l’energia cinetica media di una qualsiasi particella classica, E = 3/2kT = 3/2 ´ 300K ´ 8,6 ´ 10^-7eV/K = 0,04 eV.

Cerchiamo ora di capire perché i  neutroni termici e non quelli dotati di E superiori, cosiddetti veloci. Per farlo dobbiamo  analizzare come avviene la scissione del nucleo in due frammenti ed affrontare l’analisi di altri concetti già incontrati nel 1° livello, ma che necessitano di ulteriori precisazioni.

La  sezione d’urto

Questo concetto è proprio della teoria degli urti e quindi inquadrabile nella cinematica; vale però la pena di riprenderlo per adattarlo all’argomento in esame; già il nome dato all’oggetto è indicativo del significato, ma per parlare un po’ alla Fermi si può fare questa affermazione: se un neutrone lento o termico viene assorbito da un nucleo di uranio-235, il nucleo così formato può, con elevata probabilità, scindersi in due parti pressoché uguali; la sezione d’urto per questo processo è di 580 barn.

Cosa vuol dire?

È ovvio che stiamo parlando di collisioni di un proiettile-particella con un bersaglio-nucleo e che tale analisi non può non avere carattere statistico, a causa di limitate informazioni sulle posizioni reciproche e dell’elevato numero di interazioni.

Partiamo da un caso più semplice: alcune frecce sono indirizzate contro un bersaglio, ma, tra i vari spicchi colorati che lo compongono, si devono colpire solo quelli di colore verde. Calcoliamo la probabilità che un colpo vada a segno: (numero di spicchi di quel determinato colore)´( area di ogni singolo spicchio)/area totale del bersaglio (niente di più che la solita definizione di probabilità casi favorevoli/casi possibili). Il numero di successi nei lanci sarà dato dal prodotto tra questa probabilità e la frequenza dei lanci; quindi se lancio 10 frecce al secondo, con una probabilità di colpire con successo del 50% andranno a segno, ovviamente, 5 frecce al secondo! La sezione d’urto di questo fenomeno è rappresentata dall’area dello  spicchio verde che potremmo ipotizzare di non conoscere, ma di saper ricavare dalle altre informazioni date, applicando la formula inversa:

Lasciamo le frecce per i neutroni; ora possiamo costruire una semplice formula relativa alla sezione d’urto efficace di un evento costituito da un fascio di neutroni incidenti su un foglio metallico di area A e spessore d: n è il numero di nuclei disponibili per volume, nAd è il numero totale di bersagli del foglio; s l’area efficace del fenomeno, cioè ‘la zona che il neutrone può colpire per far centro’; nAds/A  è l’area efficace totale e nAds/A è la probabilità di colpire con successo; R₀ è la frequenza dei neutroni che sono sparati contro il foglio; R il numero di collisioni neutrone-nucleo avvenute. Allora

Nel mondo microscopico non si può parlare di m², ma di sottomultipli e di una unità di misura che è il barn = 10^-28 m²

Ritorniamo a Fermi ed all’assorbimento di un neutrone lento da parte di ²³⁵ U, evento che con elevata probabilità può dar luogo ad una scissione in due nuclei pressoché uguali: la sezione d’urto si è già detto valere 580 barn. Ora che il significato di questa affermazione è un po’ meno oscuro, dai dati del problema :

R₀  = 3´10¹⁶ neutroni/m²×s     d = 5´10^–4 cm        densità U = 18,9 g/cm³     peso atomico = 238 g/mole

percentuale di ²³⁵U = 0,72% dei nuclei

possiamo lasciare che gli studenti, per esempio, calcolino il valore di R!

Un’applicazione del genere, peraltro semplice, può essere utile agli studenti per non cadere in un possibile fraintendimento, cioè che la sezione d’urto altro non sia che l’ampiezza della sezione geometrica del nucleo bersagliato; troppe parole spese a vuoto se così fosse!!

Il nucleo di uranio ha  una sezione ‘geometrica’ di 1,4 barn , mentre il dato nel problema è ben  superiore e quindi l’analogia, con tali numeri, si dimostra presto insostenibile.

È opportuno ribadire che, nonostante abbia le dimensioni di un’area, la sezione d’urto efficace è una misura della probabilità di interazione proiettile-nucleo, essa indica l’area efficace del bersaglio collegata alla probabilità che l’evento ‘urto’ si realizzi e si comprende possa dipendere da fattori legati alle particelle incidenti, come l’energia cinetica; inoltre l’uranio-238, meno soggetto a fissione da parte di neutroni lenti, ha, a confronto, una sezione d’urto di soli 0,5 millesimi di barn, nonostante abbia dimensioni geometriche simili all’altro isotopo ‘più importante’. Per questa proprietà è spesso definito ‘non fissile’ perché, colpito da neutrone, dà luogo ad altri tipi di reazioni di cui parlerò nel paragrafo “Il plutonio”.

La  fissionabilità

Per concludere il discorso sul perché preferire i neutroni termici, possiamo analizzare questa tabella:

L’energia di eccitazione è relativa al nucleo che ha assorbito il neutrone termico, cioè l’energia di legame dell’ultimo neutrone, che possiamo immaginare caduto dentro la buca di potenziale (*) creata dalle forze nucleari e che ha trasformato l’energia potenziale in energia di eccitazione interna; nel modello a goccia questa fase corrisponde alle violente oscillazioni del nucleo mentre assume una forma allungata.

Per la scissione in due frammenti bisogna che l’energia di eccitazione superi quella di attivazione, che è un po’ come il livello minimo che serve per innescare il processo di rottura della goccia-nucleo in due gocce; solo laddove la differenza è positiva, la fissione da neutroni termici può avvenire con valori elevati di sezione d’urto; nei due casi negativi, la sezione d’urto è, ovviamente, molto piccola, ed affinché avvenga fissione è necessario che il neutrone sia ‘veloce’, cioè altamente energetico.

L’instabilità di un isotopo bombardato è dovuta al fatto che il suo nucleo è eccitato poiché ha un maggior contenuto di energia rispetto all’isotopo originario, la quale, non bisogna dimenticare, deriva dalla diversità delle masse in gioco nei due stadi. Infatti, facciamo qualche somma per rendercene conto:

massa di ²³⁵U = 235,1170 u.m.a. (**)

massa di ²³⁶U = 236,1191 u.m.a.

massa del neutrone = 1.009 u.m.a.

calcoliamo la variazione delle masse :  Dm = 235,117+ 1,009-236,1191 = 0,007 u.m.a.

Con la relazione einsteniana possiamo calcolare a quale energia corrisponda questo eccesso di massa e si arriva (omettendo ovviamente i passaggi che potrebbero invece essere utili nella trattazione al gruppo classe)  ad un valore di 6,5 MeV: può ben iniziare ad oscillare violentemente un nucleo così eccitato!!

L’energia di disintegrazione

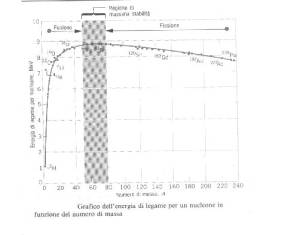La differenza tra l’energia dello stato iniziale, quando il nucleo è compatto, e quella dei due frammenti separati è l’energia di disintegrazione ed è interessante sottolineare come queste quantità in gioco siano ben superiori a quelle incontrate nelle trasformazioni chimiche; per sviluppare questo  aspetto è necessario avere sotto gli occhi il diagramma che rappresenta la curva delle energie di legame (riportato sulla quasi totalità dei testi scolastici ) ed analizzare almeno un esempio di processo di fissione.

I processi sono diversi da elemento ad elemento, però il numero di massa dei due nuovi nuclei formati è sempre pari a circa la metà di quello originario, per cui le specie atomiche prodotte non sono mai ‘vicine’ all’elemento scisso; l’U e le altre sostanze fissionabili si trovano nel grafico suddetto nelle ultime posizioni a destra, avendo un’energia di legame per nucleone di circa 7,5 MeV; i prodotti della fissione hanno un numero di massa mediamente intorno al 100 e sono posizionati nella parte più alta della curva, dove le energie sono intorno a 8,4 MeV.

La trasformazione

Nucleo di U ® due nuclei più leggeri

incrementa l’energia di legame, cioè la stabilità dei nuclei, diminuisce la massa, produce emissione di energia che vale circa:

E = (8,4-7,5) MeV ´ 235 ~ 210 MeV    (abbiamo considerato il numero di massa dell’U)

Questo è un valore medio però indicativo dell’ordine di grandezza delle E emesse; facile calcolare quanto possa ‘rendere’ un kg di U!

I  neutroni emessi

Nel Racconto ho già avuto occasione di sottolineare quanto sia importante non solo l’emissione di neutroni in seguito a fissione, ma soprattutto il numero di essi. Ritorno ancora sull’argomento.

Un generico evento di fissione di U può essere schematizzato così:

²³⁵U + n ® ²³⁶U ® X + Y + bn

dove il fattore b rappresenta il numero medio di neutroni liberato in ogni evento e vale circa 2,5. Il fatto che queste  particelle vengano espulse permette l’innesco della reazione a catena, il controllo del loro numero permette l’utilizzazione del fenomeno in chiave ‘pacifica’.

Ovviamente non tutti i valori sono equiprobabili per i numeri di massa delle sostanze X o Y, ma analizzando un altro grafico significativo (frequente anch’esso nei testi), cioè quello della distribuzione dei numeri di massa dei frammenti di U, si vede che i numeri più probabili sono intorno a 95 e 139; inoltre il rapporto neutroni/protoni del nucleo che  fissiona è ~ 1,6  e tale tende a mantenersi anche per i frammenti.

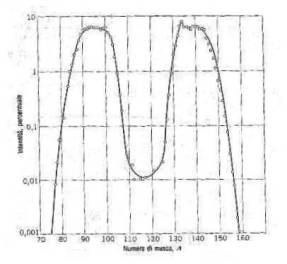
Però guardando alla curva di stabilità (anch’essa presente in tutti i testi ) si nota che tale rapporto per i nuclei che si sono formati (e per tutti quelli con numero di massa tra 75 e 150) vale 1,2 ¸ 1,4 .

I frammenti primari sono dunque troppo ricchi di neutroni ed alcuni di questi sfuggono dai nuclei, in numero appunto di 2,5 per evento di fissione; gli altri neutroni ancora in soprannumero nei frammenti verranno emessi per decadimento b ^-.

 Vorrei analizzare infine quest’ultima tabella in cui si evidenzia come si distribuisce l’energia (i 200 MeV di cui sopra) tra i prodotti della fissione, soprattutto per avere un quadro globale di tutti gli eventi associati ad essa:

Il  plutonio

Abbiamo già citato le percentuali presenti in natura dei due isotopi dell’U e precisato in relazione ad essi l’uso dei neutroni termici o veloci. Fin dai tempi della progettazione della bomba furono realizzati impianti in cui si separava il 235 dal resto del materiale, ma il rapporto costo/efficacia sottolineò subito il bisogno di risolvere diversamente il problema combustibile.

L’isotopo 238 non è del tutto inutilizzabile: se sottoposto a bombardamento da parte di neutroni lenti si forma il ²³⁹U, nucleo radioattivo che, per emissione b ^-, diventa ²³⁹Np, anch’esso radioattivo; esso si trasforma in ²³⁹Pu per decadimento b ^- ed avendo un tempo di dimezzamento lunghissimo può essere separato dall’U ed ottenuto in grandi quantità. Questo isotopo del plutonio ha il vantaggio di subire facilmente fissione indotta da neutroni lenti, con sezione d’urto maggiore rispetto allo stesso U. Il panorama dei ‘combustibili’ si completa con l’aggiunta del ²³²Th (che con un processo analogo dà ²³³U, fissile) e che insieme all’²³⁸U è detto materiale fertile.

Progettazione di un reattore

La fissione ha sul piano pratico un interesse maggiore di quello delle altre reazioni nucleari perché è realizzabile ed utilizzabile a livello macroscopico. Abbiamo parlato di quei 2,5 neutroni che, in media, sono emessi pero ogni nucleo scisso: su questo dato bisogna però meditare perché, se vogliamo conteggiare quanti neutroni sono realmente a disposizione per innescare altri processi,  non dobbiamo dimenticare che nel numero 2,5 sono compresi:

• il neutrone ‘incidente’ (che torna ad essere attivo),

• la percentuale di neutroni che ‘sfuggono’ (preciserò meglio questo concetto),

•  i neutroni ‘guadagnati’ effettivamente dalla reazione.

Ora, se dei 2,5 neutroni, per varie cause, ne rimane 1 solo in grado di fissionare un altro nucleo, allora la reazione a catena ha luogo, ma si mantiene, in condizione cosiddetta critica; se, sempre in media, rimane meno di 1 neutrone attivo, allora la reazione finirà per arrestarsi; se rimarranno più di 1 neutrone disponibile alla reazione successiva, allora il fenomeno è in accelerazione.

Il primo caso è quello in cui si trova un reattore nucleare, all’interno del quale la potenza nucleare viene mantenuta a livelli costanti e volutamente scelti; nell’ultimo caso l’energia associata al fenomeno è in aumento, in modo incontrollato, e questa modalità è alla base del funzionamento della bomba ‘atomica’.

È importante riflettere sul fatto che anche le dimensioni del ‘carburante’ fissile hanno un ruolo essenziale, come avremo modo di verificare nelle prossime analisi.

La realizzazione pratica di un reattore oppure il raggiungimento della soglia di criticità per un ordigno bellico, non è cosa facile per fortuna, e la Storia delle scoperte fisiche (come nel Racconto) ci ha fatto capire che in queste prove si vede la differenza tra chi riesce e chi tenta, tra chi segue una logica e chi spera nel caso. Fermi in questo insegna più di tanti altri.

Il problema da risolvere è questo: come riuscire ad ‘imbrigliare’ i neutroni emessi dai frammenti?

È già noto che procurare del buon combustibile ‘fissile’ o reso tale è molto difficile; in più queste particelle hanno la tendenza a sfuggire, a disperdersi all’esterno, ad essere assorbiti dalle impurità, così che quel valore 2,5 medio perderebbe tutto il suo significato.

Allora servono accorgimenti di vario tipo.

Iniziamo col dire che viene impiegato U arricchito: questo significa che viene artificialmente accresciuta la percentuale di ²³⁵U presente nel campione scelto, per poter lavorare con i neutroni termici. Inoltre, nonostante i neutroni che dall’esterno colpiscono il campione siano appunto termici, quelli fuoriusciti dai frammenti hanno energie più elevate, intorno ai 2 MeV, ed in queste condizioni non potrebbero assicurare altre fissioni; allora si rende necessario rallentarli, affinché perdano energia cinetica senza, però, essere assorbiti.

Questa è la funzione del moderatore, che può essere liquido ( H₂O, D₂O ), solido (grafite), gassoso (CO₂), comunque sostanza costituita da atomi leggeri, i quali danno luogo ad urti elastici con i neutroni diminuendone l’energia.

Per evitare l’assorbimento, anche da parte della struttura stessa del reattore, e la fuoriuscita delle particelle, dannosa anche per l’uomo, il nucleo di U o Pu viene circondato da un riflettore, il quale respinge i neutroni che altrimenti sfuggirebbero: questo accorgimento riesce ad incidere anche sulle dimensioni del nocciolo che possono diminuire se la ‘perdita’ dei proiettili è contenuta.

I neutroni veloci fuoriusciti dai frammenti rischiano però, prima di essere totalmente ‘moderati’, di venire assorbiti (si chiama cattura di risonanza) dai nuclei di ²³⁸U senza spaccarli, ma producendo solo emissioni di raggi g. Per evitare questa ulteriore difficoltà strutturale Fermi pensò di intramezzare ai mattoncini di uranio lo stesso moderatore, affinché il neutrone attivo avesse maggiore probabilità di incontrare sulla sua strada la grafite prima degli altri nuclei da fissionare, favorendo il rallentamento e non l’assorbimento. Combustibile e moderatore possono essere intimamente mescolati, come nelle soluzioni di sali di U in acqua pesante, o nettamente separati, come nella prima Pila realizzata.

Certo non è stato facile individuare la disposizione geometrica ottimale per combustibile e moderatore (c’è un riferimento a questo problema nell’articolo del prof.Gandini), tuttavia possiamo riferirci alla fig.2 di pag.188 del libro “Conoscere Fermi” ed all’ultima figura del Racconto per comprendere la soluzione scelta.

 Ed ora parliamo delle dimensioni: ho sottolineato in precedenza che il numero di particelle neutroniche emesse è un effetto di volume ( immaginiamo per comodità un blocco sferico) e quindi proporzionale al cubo del raggio; il numero delle particelle che sfuggono è invece un effetto di superficie, cresce con essa, e quindi proporzionale al quadrato del raggio; dunque il rapporto superficie/volume = 3/r può essere diminuito aumentando la lunghezza del raggio, cioè ingrandendo il nocciolo. Infatti un kg di ²³⁵U o di ²³⁹Pu hanno le dimensioni di una pallina da golf e non potrebbero mai esplodere perché, seppure un nucleo subisse fissione, i neutroni farebbero prima a fuggire dalla piccola superficie che ad innescare un altro processo! Se il peso fosse di 16 kg, le dimensioni sarebbero diverse e la massa critica.

Quanto detto vale ovviamente per ogni blocco di carburante che costituisce il nucleo del reattore ed è valso anche al calcolo delle opportune dimensioni dell’uranio usato dal gruppo di Fermi a Chicago per raggiungere le criticità della ‘bomba’.

Sempre nel già citato articolo, si fa riferimento al cosiddetto fattore di criticità, indicato con k, che in una trattazione più semplice dell’argomento si può definire come il rapporto tra il numero di neutroni che si producono in ciascun ciclo di fissione / quelli presenti all’inizio del ciclo. Ho già parlato di questi valori, ma introducendo k aderisco alla notazione ufficiale e si semplifica la scrittura. Usualmente se

k = 1      reattore critico

k < 1     reattore sottocritico

k > 1      reattore supercritico

Ricordiamo sempre che il valore di k dipende da tutti quei fattori analizzati in precedenza.

Ovviamente per realizzare una esplosione nucleare bisogna disporre di un k maggiore di 1 e quindi di una massa supercritica. Quanto tempo avremmo a disposizione ……….per fuggire?

Molto poco, non basterebbe neppure per pensare: la produzione di energia è di tipo ‘esponenziale’, come ci viene spiegato nel Libro, frazioni impercettibili di secondo ci separerebbero dall’esplosione; allora è meglio separare la massa critica in due parti e tenerle ben distanti !

Il sistema più semplice è infatti quello di utilizzare due (o più) pezzi, ciascuno di dimensioni subcritiche, che vengano sparati violentemente uno contro l’altro da propellenti chimici; così furono fatte detonare le bombe del 1945.

Però le tecniche più recenti seguite per la preparazione del combustibile propongono un sistema diverso, chiamato dell’implosione: partiamo da una sfera di massa M , volume V, densità r di materiale al limite di criticità; un neutrone generato nella zona centrale del materiale ha una probabilità del 50% circa di fissionare  prima di fuoriuscire.

Se il tutto viene compresso per raddoppiare la densità del combustibile, il raggio r della sfera diminuisce di (2)^1/3 (circa 0,8 volte minore), il neutrone interno, in uscita, incontrerà una densità doppia di atomi  e la probabilità di provocare fissione aumenterà rendendo un complesso di massa quasi critica supercritico.

Ma anche i reattori delle centrali nucleari sono progettati, come quello di Fermi, per essere supercritici, anche se non sono esposti a rischio  esplosione grazie alle barre di controllo di cui abbiamo già letto nel Racconto. Infatti con il loro opportuno posizionamento, si passa dalla supercriticità alla criticità, per qualsiasi livello di potenza al quale si vuole lavorare e compreso nel range di funzionamento del reattore.

Abbiamo letto che Fermi ‘giocava’ con l’estrazione delle barre di cadmio in relazione alla potenza raggiunta dal reattore, più lui dei suoi collaboratori, poiché conosceva bene un’altra variabile del funzionamento dell’impianto: la risposta temporale.

Essa consiste nel tempo che impiega il reattore per aumentare il livello di potenza man mano che la sbarra viene estratta. Infatti, per una struttura complessa come quella descritta nell’articolo, i tempi di espulsione dei neutroni non sono irrimediabilmente piccoli; i neutroni emessi per decadimento b  dai frammenti hanno dei ritardi nel fuoriuscire dovuti a tempi di dimezzamento che vanno da 0,2 a 50 secondi. Queste particelle sono una frazione piccola di tutte quelle che investono i nuclei, però abbastanza significativa da permettere di confrontare i tempi del reattore con i riflessi dell’uomo.

Riferimenti bibliografici

Il titolo scelto per la rielaborazione degli articoli, ‘Enrico Fermi e l’energia nucleare: un argomento poco trattato’, non è stato casuale: infatti nella fase di reperimento materiale per realizzare questa stesura 'didattica’, mi sono resa conto che la fissione spesso occupa poco più di un paragrafo nei libri di testo più comuni, e le informazioni sono compresse,  presentate in linee generali e non armonicamente correlate tra loro.

Lo scarso successo nei curricoli scolastici ha una ulteriore motivazione.

Questa proposta didattica non è certo esaustiva, ma penso di avere almeno citato gli elementi essenziali da toccare in una trattazione semi-quantitativa.

Devo ricordare che qualche spunto di maggiore interesse l’ho incontrato in due testi piuttosto datati, La fisica e l’universo fisico – J.B.Marion e Temi fondamentali della fisica moderna – S.Morettini , in Fondamenti di chimica – P. Silvestroni ed  in Fondamenti di fisica – D.Halliday, R.Resnick.