Si tratta di una domanda che molti vorrebbero rivolgere ai fisici. La risposta può essere complicata da dare, ma bisogna riconoscere loro che hanno fatto del problema della previsione di quanto accadrà uno scopo di vita, lavorando al rapporto causa-effetto, sia pure con alterne vicende, con tutti i mezzi a loro disposizione.

Partiamo da un personaggio di sicuro rilievo.

Che risposta darebbe Newton?

Se consideriamo la sua descrizione del mondo ci accorgiamo che essa è classificabile come descrizione deterministica: ogni evento ha una causa della quale esso è l’effetto¹. Per trovare la causa è necessario conoscere le condizioni iniziali²; queste, a loro volta, sono effetto di altre cause e, risalendo all’indietro, ancora di altre cause, fino ad arrivare alle Condizioni Iniziali per eccellenza, che sono delle condizioni delle quali un fisico non si chiede come siano state prodotte; non gli interessa e non spetta a lui rispondere a certe domande.

Newton studia il moto di un sistema di corpi, disinteressandosi di quali corpi siano: possono essere indifferentemente palle da biliardo che si urtano o pianeti. Dal suo studio derivano le tre leggi della Dinamica, che governano completamente il comportamento degli oggetti materiali. L’universo di Newton è composto da oggetti che si muovono seguendo queste leggi nello spazio euclideo. Essi si muovono con accelerazione determinata dalla risultante delle forze che agiscono su di essi, forze che sono determinate a loro volta da azioni che derivano dalla presenza di tutti gli altri oggetti esistenti. La composizione vettoriale è l’operazione matematica che ci permette di ricavare la forza totale applicata.

Avendo contemporaneamente intuizioni fisiche di grande rilievo e notevoli capacità matematiche, Newton costruisce un sistema preciso e determinato di equazioni dinamiche, dalle quali si possono derivare alcuni dei risultati già noti nel suo tempo (per esempio le tre leggi di Keplero...). Si tratta dei fondamenti della Meccanica classica.

Da una semplice occhiata alla struttura matematica delle leggi di Newton, si ricava la sua ipotetica risposta al nostro quesito. Essa è affermativa naturalmente e così articolata: dato un qualsiasi sistema di corpi³  (un tavolo da biliardo o il sistema solare), una volta note le posizioni e le velocità dei singoli elementi del sistema in ogni singolo istante, il comportamento del sistema stesso è rigorosamente determinato nel futuro.

Per esempio, se conosciamo le coordinate spaziali e le velocità di tutti i pianeti del sistema solare in un istante assegnato, siamo in grado di descrivere lo stato del sistema in ogni momento successivo a quello considerato, utilizzando le equazioni di Newton. In sintesi se si è in possesso di informazioni sufficienti, è possibile “prevedere il futuro” di un sistema di corpi, usando i modelli della Meccanica newtoniana⁴.

Dice Penrose: “Questa forma di determinismo...esercitò...una profonda influenza sul pensiero filosofico. Cerchiamo di esaminare questo determinismo newtoniano un po’ più da vicino. Che cosa può dirci sulla questione del “libero arbitrio”? Un mondo rigorosamente newtoniano potrebbe contenere delle menti?”.

Lasciamo ad altra sede la discussione di quesiti come questi e andiamo ancora un po’ avanti nel tempo.

Ma che cosa è accaduto da Newton in poi? La Meccanica statistica.

Dopo che Newton ebbe elaborato le equazioni del moto, si è pensato a lungo che la previsione del moto di un pianeta, (per usare sempre lo stesso esempio), fosse un problema, e un problema anche abbastanza semplice, di matematica applicata: sarebbe bastato inserire i dati in alcune equazioni differenziali, a patto che fossero ben poste, e successivamente integrarle. A questo punto i fisici hanno dapprima impostato queste equazioni per sistemi sempre più complessi⁵, pensando che esse sarebbero state risolte, calcolando così gli integrali o invarianti del moto. Alla domanda “sarà sempre possibile farlo?” essi avrebbero risposto di si, aggiungendo: a patto che il matematico che se ne occupa sia abbastanza bravo, tutte le descrizioni meccaniche sono integrabili, cioè tali da fornire soluzioni esatte. Per poter predire il futuro, infatti, bisogna che questo futuro esista già nelle condizioni presenti, ma anche che lo si possa “calcolare”, che esso sia cioè computabile⁶.

Verso la fine dell’’800, alcuni grandi nomi della storia della fisica studiano il comportamento di sistemi di particelle microscopiche. Gli studenti di quinta classe conoscono già questi personaggi:
L. Boltzmann, il papà della teoria cinetico-molecolare dei gas, J. C. Maxwell (il suo tentativo di connettere comportamento molecolare e viscosità fu paragonato da Boltzmann ad un “grande poema sinfonico”), Albert Einstein con le sue indagini sui moti browniani.

Occorre ricordare che, fin dall’inizio, il microscopico crea problemi in più, rispetto ai sistemi della meccanica newtoniana. Come possiamo guardare al microscopico? Ipotizzando che le particelle siano sfere rigide che si urtano in modo perfettamente elastico e alle quali possiamo applicare le equazioni newtoniane, presupponendo che tutte le forze agenti su di loro siano funzioni delle distanze fra i centri delle varie particelle e dirette lungo le congiungenti dei centri stessi. Quindi utilizzando i metodi della Meccanica di Newton?

Stavolta la risposta è negativa: il modello newtoniano non è applicabile a sistemi formati da un elevatissimo numero di particelle, come per esempio le molecole di un gas perfetto Si tratta di uno strumento inadatto e complicato da usare per sistemi costituiti da così numerosi elementi.

Nasce allora la Meccanica statistica e proprio il gran numero di particelle (la legge dei grandi numeri) obbliga ad usare le leggi del calcolo delle probabilità per mettere in relazione grandezze microscopiche e variabili macroscopiche. Il modello però è ancora quello delle sfere rigide e gli urti sono gli urti di due sole sfere rigide alla volta.

Se riflettiamo sulla evoluzione dei metodi matematici di analisi dei sistemi, sappiamo già che se rivolgessimo a Boltzmann e Maxwell la domanda rivolta idealmente a Newton, essi ci risponderebbero, usando un linguaggio diverso: determinando i valori medi di certe grandezze microscopiche calcolate su un campione di tanti microstati equivalenti e associandoli alle corrispondenti grandezze macroscopiche, introducendo il principio di equipartizione dell’energia, la definizione della probabilità di uno stato come frequenza di raggiungimento di quello stato, il concetto di entropia come caratteristica di un macrostato che risulta avere valore tanto maggiore, quanto più grande è il numero di microstati ad esso associati,.............è possibile.

Insomma per dirla con un solo termine, ci risponderebbero con il linguaggio della Meccanica statistica, ma, pur con un linguaggio diverso⁷, la risposta sarebbe affermativa.

In conclusione, Boltzmann e compagni ci risponderebbero ancora di sì nei termini seguenti:

E se si verificassero urti a tre?

Qui la risposta cambierebbe radicalmente. Ci troviamo, infatti, in una situazione non deterministica.

Potremmo ancora cavarcela affermando, per esempio, che le collisioni a tre sono molto improbabili e quindi non considerandole, ma dovremmo comunque riflettere sul fatto che, anche se molto poche se ne verificano, esse esistono e le conseguenze si leggono nello stato dell’intero sistema.

Allora, cosa rispondere alla domanda: i fisici possono prevedere il futuro?

Nel 1889, un grande della matematica, Henry Poincaré, fornisce alcune risposte. È un buffo personaggio, che coincide stranamente con lo stereotipo del matematico da fumetto: goffo nei movimenti, distratto, continuamente alla ricerca dei suoi occhiali che poi si ritrova sul naso, ma un suo insegnante dice di lui diciottenne: ho in classe, a Nancy, un mostro di matematica...

Ebbene, proprio un matematico⁸, anzi per dirla con il suo insegnante, un mostro di matematica, dimostrando due teoremi, “mette in crisi” sia la Meccanica newtoniana che la Meccanica statistica.

Egli dimostra che, non appena cerchiamo di analizzare il moto di tre corpi, per esempio il Sole, la Terra, la Luna, ci troviamo di fronte ad un sistema intrinsecamente non integrabile, che è un modo per dire che non è possibile risolvere esattamente il problema mediante l’analisi matematica. Figuriamoci cosa succede per le molecole di un gas. La meccanica newtoniana, accompagnata dal suo implicito determinismo riceve un bel colpo⁹.

Ma Poincaré fa di peggio; dimostra il teorema di ricorrenza (spesso citato come teorema dell’eterno ritorno): come conseguenza delle leggi della meccanica newtoniana, un sistema isolato e confinato in una regione finita di spazio, ritorna infinite volte in uno stato arbitrariamente vicino a quello iniziale.

E questo liquida anche la Meccanica statistica, con la sua entropia sempre crescente, la teoria della morte termica dell’universo, etc...: un disastro, una débacle totale.

Eppure non si tratta di una débacle definitiva se si fanno le opportune distinzioni, ma ne riparleremo. Intanto, possiamo precisare meglio il ruolo della variabile tempo nel teorema di Poincaré, il che ci è utile a quantificare quel tanto che basta per capire la ricaduta dei suoi teoremi sulla trattazione fisica dei sistemi: un sistema costituito da un grandissimo numero di particelle, ha un tempo di ricorrenza superiore di molto l’età attuale dell’universo, cioè di 10¹⁰ anni, il che vuol dire che della cosa ci si può anche disinteressare.

I sistemi ergodici.

Vediamo di sintetizzare la situazione. Se sto considerando il moto di un pendolo semplice¹⁰, con una piccola ampiezza di oscillazioni, esso costituisce di sicuro un sistema integrabile e le equazioni newtoniane del suo moto hanno soluzioni esatte. In più non ho difficoltà a pensare che esso osservi la regola del teorema di ricorrenza di Poincaré, perché il moto del pendolo si ripete “senza fine” e si vede. Si tratta di un sistema deterministico.

Proviamo ora con le molecole di un gas chiuso in un contenitore isolato. Esse si urtano fra loro e con le pareti del recipiente perché si muovono in modo casuale; possiamo ragionevolmente pensare che ogni molecola, con il passare del tempo esplorerà tutto il contenitore e probabilmente riassumerà anche tutte le possibili velocità con un unico vincolo, che l’energia totale rimanga costante.

I sistemi che hanno questo tipo di comportamento si chiamano sistemi ergodici.

Una metafora simpatica e chiara per definirli è quella descritta da P. Coveney nel libro La freccia del tempo: “una “scimmia ergodica” immortale, che battesse all’impazzata sui tasti di una macchina da scrivere in un tempo inimmaginalmente lungo scriverebbe tutte le opere di Shakespeare e, insieme ad esse, tutte le opere di Dickens e di ogni altro scrittore”¹¹.

Si occupano dello studio di sistemi come questi Boltzmann, Gibbs ed anche Maxwell; quest’ultimo ne esprime così le proprietà con il linguaggio della Meccanica statistica: “...il sistema se abbandonato a se stesso nel suo presente stato di moto, passerà presto o tardi attraverso tutte le fasi che sono in armonia con l’equazione dell’energia”.

Una volta definiti i sistemi ergodici, anche se in modo indiretto¹², occorre costruire una teoria matematica rigorosa che li riguardi: cominciano a lavorarci, negli anni trenta, matematici come John von Neumann, George Birkhoff ed Halmos, ad esempio. L’argomento è poi diventato una branca della matematica pura¹³, nell’ambito della quale i principali artefici sono alcuni matematici russi, per esempio Kolmogorov, Anosov, Arnold e poi Sinai.

Ma parliamo ancora di sistemi ergodici.
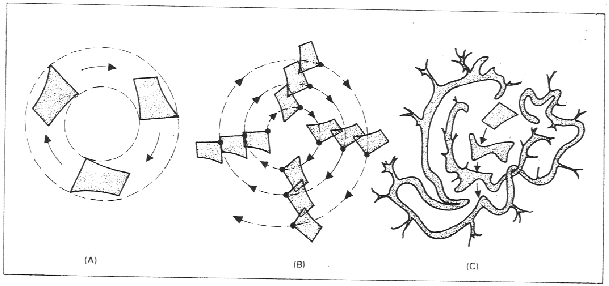
Cosa succede se ipotizziamo piccoli mutamenti delle condizioni iniziali di un sistema? La regola per i sistemi deterministici è espressa dalla (1). Qui la regola è:
Se si cambiano di pochissimo le condizioni iniziali, cambia del tutto l’evoluzione del sistema (2).

Quando accade questo si dice che il sistema dinamico è caotico¹⁴; un sistema dinamico è caotico, quando è altamente instabile. Un flipper è un buon esempio di sistema instabile; potremmo cercare di riprodurre con la massima precisione possibile l’impulso dato dal giocatore all’inizio della partita alla pallina d’acciaio, ma il flipper darebbe per ogni partita un risultato diverso.

A questo punto il determinismo alla Newton ci mette un po’ in sospetto. A che punto siamo con la domanda: possono i fisici prevedere il futuro?

Una risposta completa non l’abbiamo ancora ricavata, ma la (2) ci dice implicitamente che qualunque incertezza presente all’inizio di un fenomeno, fa saltare la possibilità di prevedere il futuro.

L’opinione di E. Fermi.

Fermi si inserisce nel discorso dei sistemi dinamici nel 1923, argomentando che: se un sistema non è integrabile è ergodico¹⁵. Mentre i matematici continuano a trattare il problema in modo totalmente astratto, la comunità dei fisici accetta l’idea che alcuni teoremi sulla non esistenza di integrali delle equazioni del moto implichino l’ergodicità. Fermi tornerà sull’argomento molti anni dopo.

Enrico Fermi aveva lavorato per anni al progetto Manhattan presso il centro di Los Alamos, a contatto con von Neumann ed aveva già avuto modo di rendersi conto delle potenzialità dei primi calcolatori elettronici. A Los Alamos c’era uno dei primi esemplari di calcolatore, primitivo rispetto a un esemplare moderno. Dopo la guerra, Fermi, che vuole tornare alla ricerca sperimentale, si reca spesso a Los Alamos, occupandosi fra l’altro di Meccanica statistica. Lavora con J. Pasta e S. Ulam ed è proprio Ulam a raccontarci di come egli cominci ad interessarsi ad un utilizzo dei computer estremamente moderno ed originale, applicato alla ricerca scientifica.

Fino ad allora, il computer era stato considerato una macchina che effettua velocemente calcoli difficili con numeri a molte cifre, una enorme calcolatrice, insomma. Fermi, sempre alla ricerca di nuove frontiere, (cita ironicamente Mussolini “O rinnovarsi o perire”), concepisce la portata dell’utilizzo del calcolatore per simulazioni numeriche funzionali alla ricerca¹⁶. In particolare lui e Ulam decidono di usarla per analizzare i comportamenti dinamici di sistemi non lineari. Sono dei precursori. Dopo di loro lo faranno molti ricercatori a partire dagli anni sessanta e settanta.

Dal lavoro di quegli anni a Los Alamos deriva la pubblicazione, postuma per Fermi, (1965) dell’articolo Studies of non linear problems, noto fra gli esperti del settore con la sigla FPU (Fermi, Pasta, Ulam), sigla che diventerà poi sinonimo di sistema integrabile perturbato.

In esso si prende in considerazione un sistema formato da una catena di particelle uguali collegate fra di loro da molle non lineari¹⁷. Fermi e Ulam si aspettano il risultato previsto dalle leggi della meccanica statistica: il sistema si evolverà da una situazione in cui tutta l’energia è concentrata in un solo modo, ad una situazione di equipartizione dell’energia; ciò dovrebbe avvenire dopo un tempo che viene denominato tempo di termalizzazione per analogia con i fenomeni termici, ma che viene denominato anche tempo di rilassamento; questo tempo potrà essere lungo, ma una volta trascorso, si sarà arrivati ad una situazione di equipartizione.

Fermi non ha dubbi sul risultato e imposta la simulazione per misurare i tempi di rilassamento, mentre non pensa neanche a controllare la sua dimostrazione dell’ipotesi ergodica.

Ulam racconterà nel 1976, come gli scienziati avessero simulato sul nuovo computer MANIAC a Los Alamos l’evoluzione di un sistema dinamico molto semplice: una corda vibrante, con “risultati del tutto diversi da quelli che persino Fermi, con la sua grande conoscenza dei moti ondulatori, si era atteso...la corda cominciò a suonare una sorta di gioco dei quattro cantoni... ”¹⁸.

Il lavoro sperimentale al calcolatore costituisce per Fermi una grossa sorpresa: per un sistema perturbato, le simulazioni non evidenziano alcuna traccia di tendenza all’equipartizione, anche dopo tempi molto lunghi; accade cioè che Fermi legge sperimentalmente la violazione dell’ergodicità e del mescolamento. 

I risultati sono in contraddizione con le aspettative¹⁹: sembra che, dopo un tempo sufficiente lungo, il sistema ritorni allo stato iniziale. Proprio così: invece di perdere la memoria della sua situazione iniziale, ritorna, anche se dopo lungo tempo, ad essa.

È l’eterno ritorno di Poincaré? Fermi rimane spiazzato, consapevole che si trova davanti ad una grande scoperta. Vorrebbe parlarne in una prestigiosa conferenza scientifica della American Mathematical Society nel 1955, ma a causa della malattia che lo porterà alla morte non terrà mai questa conferenza.

Una domanda ancora attuale.

Fermi non avrebbe dato una risposta alla domanda del titolo, ma, conoscendolo, si sarebbe messo al lavoro per indagare ulteriormente sulla questione²⁰.

La soluzione del problema era stata trovata nel 1954, all’insaputa di Fermi e Ulam, dal matematico russo A.N. Kolmogorov che con i colleghi Arnold e Moser enuncerà poi il teorema indicato in gergo con la sigla KAM²¹. 

Kolmogorov studia sistemi che mostrano un comportamento ancor più caotico dei sistemi dinamici ergodici instabili. Per dirla il più semplicemente possibile, si tratta di sistemi il cui comportamento è ai limiti della imprevedibilità totale. Si può parlare di sistemi K, intendendo quelli per i quali un numero, anche infinito, di misure precedenti non consente di prevedere il risultato della misura successiva, a meno che le misure precedenti non siano state effettuate con una precisione infinita, il che è fisicamente impossibile. L’evoluzione di questi sistemi è perciò intrinsecamente casuale.

Kolmogorov studiò le proprietà di questi sistemi, ma fu il contributo di Yasha Sinai ad essere decisivo.

Molti studiosi degli anni cinquanta credono a questo punto che tutti i tipi di comportamenti descritti prima abbiano poco a che vedere con la realtà, ma che siano astrazioni matematiche pure e semplici. Nel 1962 Sinai annuncia di aver dimostrato che una scatola contenente due o più palle da biliardo si comporta come i miliardi di molecole in un gas: una partita di biliardo o di boccette può essere caotica ed imprevedibile quanto un sistema formato da miliardi di molecole di un gas che si mescolano in un recipiente. Un piccolo errore della descrizione del modo in cui la stecca colpisce la palla genera una totale incertezza sulla posizione che la palla, nel lungo periodo andrà ad occupare.

In definitiva, la domanda “i fisici possono prevedere il futuro?” è ancora attuale, ma la risposta, al momento, sembra dover essere no. E la storia continua...²²