Lezione n.0

Prerequisiti matematici

1. Distribuzioni di n oggetti in g contenitori

Queste note non hanno affatto l’intenzione di insegnare il calcolo combinatorio a persone che certamente lo conoscono meglio di me. Hanno invece lo scopo di dare all’insegnante che decidesse di affrontare l’unità una serie di esempi, una casistica di modelli concreti che gli studenti possono utilizzare per visualizzare la distribuzione delle particelle ed averne un’immagine più concreta. Hanno anche la presunzione di indicare al docente il modo più opportuno per introdurre il calcolo combinatorio in vista delle applicazioni alla meccanica statistica (i manuali sono quasi sempre carenti al riguardo: le uniche eccezioni in lingua italiana che conosco sono riportate in fondo).

Il problema fondamentale del calcolo combinatorio applicato alla fisica è semplice: contare il numero di modi in cui n oggetti possono essere messi in g contenitori. Supporremo sempre che questi contenitori siano distinguibili, cioè che sia possibile contrassegnarli in qualche modo (per esempio con un numero d’ordine, un nome, una lettera di un alfabeto) così da stabilire di quale contenitore stiamo parlando.

Possibili modelli:

1. Numero di modi in cui n oggetti possono essere messi in g cassetti;

2. Numero di modi in cui n persone possono disporsi in g stanze;

3. Numero di modi in cui i compleanni di n persone possono capitare nei g = 365 giorni dell’anno;

4. Numero di modi in cui n caramelle possono essere date a g bambini;

5. Numero di modi in cui gli n clienti di una stazione termale possono occupare i g orinatoi che circondano le fonti;

6. Numero di modi in cui le n particelle di un sistema meccanico (o termodinamico) possono distribuirsi tra i g stati dinamici del sistema.

Nei modelli descritti i g contenitori vengono considerati immobili: sono gli oggetti che vanno ad occuparli. Ma nulla vieta di considerare fermi gli oggetti e far muovere i contenitori, che vanno, per così dire, ad appropriarsi degli oggetti medesimi. Ragionando così è possibile non solo riformulare i modelli descritti precedentemente, ma anche riconoscerne l’equivalenza con quelli che seguono:

7. Numero di parole di lunghezza n che è possibile formare con un alfabeto di g lettere, chiamando "parola" un semplice allineamento di lettere, senza alcuna preoccupazione di natura semantica;

8. Numero di modi in cui è possibile sorteggiare campioni di numerosità n da una popolazione di g elementi (molto importante in statistica).

Bisogna tener presente che, in questa nuova interpretazione, il nome dell’individuo, o la lettera dell’alfabeto, corrisponde alla scelta del contenitore, mentre il numero di sorteggio corrisponde all’(eventuale) numero d’ordine dell’oggetto. Volendo scherzare un po’ la prima interpretazione potrebbe essere chiamata modello zanzara: n zanzare affamate sono pronte a gettarsi su g persone e a pungerle; la seconda interpretazione potrebbe invece essere chiamata modello mantide: g mantidi in agguato aspettano al varco n potenziali vittime per "incorporarle". In senso letterale.

Il numero di modi in cui gli n oggetti possono essere messi nei contenitori dipende da due circostanze:

1. Se gli oggetti sono distinguibili o no;

2. Se vale o no il principio di esclusione.

Dire che gli oggetti sono distinguibili significa dire che consideriamo rilevante sapere non solo quanti oggetti si trovano in ogni contenitore, ma anche quali oggetti. Gli oggetti microscopici sono indistinguibili in linea di principio (i pacchetti di onde si mescolano e non è possibile, se non in casi di estrema rarefazione della materia, seguire individualmente le particelle nel loro moto). Gli oggetti macroscopici sono invece certamente distinguibili; però, se siamo interessati solo a sapere quanti oggetti e non quali sono in un determinato contenitore, possiamo anche far finta che non lo siano.

Entriamo in dettaglio ed analizziamo i precedenti modelli.

Nel caso degli oggetti nei cassetti generalmente ci interessa sapere che cosa abbiamo messo nel cassetto n. 1, nel cassetto n. 2, ecc. In questo caso consideriamo ovviamente distinguibili gli oggetti. Però possiamo anche essere interessati a sapere quanti oggetti vi sono a prescindere dalla loro natura. In tal caso li consideriamo indistinguibili. Un esempio banale: supponiamo di dover mettere l’antitarme nei cassetti e di avere a disposizione palline di naftalina e palline di canfora, che consideriamo del tutto equivalenti. Ai fini di quel che dobbiamo fare ci interesserà sapere solo quante palline abbiamo messo in ogni cassetto, a prescindere dal fatto che siano tutte di naftalina, o tutte di canfora, o di canfora e naftalina mescolate in varie proporzioni. In questo caso decidiamo di considerare le palline indistinguibili, perché del tutto equivalenti per la funzione che devono svolgere.

Il caso delle persone nelle stanze è analogo. Generalmente le persone sono distinguibili, ma se, per esempio, si tratta di piantonare stanze di ospedale in cui sono ospitati pericolosi malviventi, al commissario incaricato della sicurezza interesserà sapere che, per esempio, nella stanza 205 sono stati messi di guardia due agenti e nella stanza 304 uno solo. Non sarà invece interessato a sapere come gli agenti Caputo, Piscopo e Currò sono stati distribuiti nelle due stanze. Il caso dei compleanni si tratta allo stesso modo.

Il caso delle caramelle è identico. Le caramelle possono avere diversa forma, colore, o sapore. Allora non sarà la stessa cosa dire che, per esempio, il secondo bambino ha ricevuto due caramelle alla menta e una all’arancia, oppure due caramelle all’arancia e una alla menta. Le caramelle possono però essere tutte uguali, e allora il bambino sarà interessato solo al numero di caramelle ricevute. Le caramelle saranno per lui indistinguibili.

Il caso dei vespasiani è leggermente più complesso perché soggetto al principio di esclusione. Nei casi precedenti non c’erano limitazioni al numero di oggetti assegnati ad ogni contenitore: questo poteva non avere oggetti al suo interno oppure averne un numero qualsiasi, fino al limite di n. Un orinatoio invece o è libero oppure, se è occupato, non può esserlo da più di una persona. Anche qui, naturalmente, gli oggetti possono essere considerati distinguibili oppure no. Per il cameriere che deve rintracciare il sig. Rossi, chiamato urgentemente al telefono, sarà importante non solo sapere se il gabinetto n. 150 è libero oppure no, ma anche chi lo occupa. Per chi deve recarsi ai servizi interessa solo sapere quali sono liberi e quali no, a prescindere da dove i sigg. Bianchi, Rossi e Neri stanno in questo momento facendo pipì.

A questo punto si possono tirare le somme: gli oggetti possono essere distinguibili o non distinguibili, soggetti o meno al principio di esclusione. Si hanno in totale quattro casi possibili.

1. Oggetti distinguibili e non soggetti al principio di esclusione. Danno origine alla statistica di Maxwell-Boltzmann. Il numero di modi in cui gli n oggetti possono essere assegnati ai g contenitori è gn. Infatti, il primo oggetto può essere messo in ciascuno dei g contenitori, e ciò può essere fatto in g modi possibili, il secondo anche, e si hanno g×g = g² modi, ecc. 

2. Oggetti distinguibili, ma soggetti al principio di esclusione. In questo caso il numero di distribuzioni è pari al numero di disposizioni di g oggetti a gruppi di n. Infatti il primo oggetto può essere messo in ciascuno dei g contenitori, in g modi diversi; il secondo oggetto solo nei g-1 contenitori non occupati dal primo, ecc. Sì hanno così g(g-1)(g-2)...(g-n+1) = D_g,n modi possibili per assegnare gli n oggetti ai g contenitori. Questa distribuzione non dà origine ad alcuna statistica, anche se trova applicazione corrente nella vita quotidiana (graduatorie di concorsi, gare sportive, ecc.).

3. Oggetti indistinguibili e non soggetti al principio di esclusione. Danno origine alla statistica di Bose-Einstein. Questo è il calcolo più complesso, e più difficile da far capire agli studenti. Conviene procedere nel secondo modo dei modi descritti: anziché tenere fermi i contenitori e metterci dentro gli oggetti teniamo fermi gli oggetti e lasciamo che siano i contenitori a scegliersi gli oggetti da contenere. Il modello più adatto allo scopo, perché più intuitivo, è quello degli oggetti e dei cassetti. Disponiamo innanzitutto gli n oggetti in fila, numerati da 1 a n. Poi stabiliamo di porre tra gli oggetti pareti divisorie mobili, che determinano la ripartizione degli oggetti nei cassetti: sono i cassetti a scegliersi gli oggetti da conservare anziché gli oggetti a scegliere i cassetti in cui andare a finire. Poiché i cassetti sono g basteranno g-1 pareti divisorie per identificarli. A questo punto abbiamo in totale n+g-1 “cosi” disposti in fila, di cui n (gli oggetti) di un tipo e g-1 (le pareti divisorie) di un altro tipo. Il numero totale di modi in cui è possibile ripartire i “cosi” è, ovviamente, (n+g-1)!. Per ottenere il numero di distribuzioni possibili bisogna osservare che bisogna considerare equivalenti due permutazioni che si ottengono l’una dall’altra mantenendo fisse le pareti divisorie e permutando gli oggetti (sono indistinguibili, quindi è irrilevante quali oggetti stiano nel primo cassetto, quali nel secondo ecc.). Allo stesso modo si devono ritenere equivalenti due permutazioni che si ottengono l’una dall’altra mantenendo fissi gli oggetti e permutando le pareti divisorie (cosa che non cambia assolutamente nulla: né la distribuzione delle palline né l’individualità dei cassetti, che è determinata dal numero d’ordine, cioè dalla posizione, e non dall’individualità delle pareti divisorie). Il numero totale di modi in cui n particelle indistinguibili possono essere messe in g contenitori, e senza esclusione, si ottiene perciò dividendo (n+g-1)! per n!, numero di permutazioni degli n oggetti, e per (g-1)!, numero di permutazioni delle (g-1) pareti divisorie. Quindi si hanno:
                                            
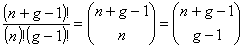
   modi possibili. Tale numero, com’è noto, è pari al numero di combinazioni con ripetizione di g elementi a gruppi di n.

4. Oggetti indistinguibili e soggetti al principio di esclusione. Danno origine alla statistica di Fermi-Dirac. Anche in questo caso conviene lasciare fermi gli oggetti e muovere i contenitori. Solo n dei g contenitori potranno "appropriarsi" di un oggetto. Ciò equivale a formare un gruppo di n elementi, da una popolazione di numerosità g, in cui non interessa l’ordine di formazione (gli oggetti sono indistinguibili: interessa solo sapere se un contenitore possiede un oggetto o no, non quale oggetto eventualmente possiede). Si hanno perciò tanti modi possibili quante sono le combinazioni semplici di g oggetti a gruppi di n.

Nell’interpretazione statistica del numero di campioni estratti, la distinguibilità o meno degli oggetti corrisponde all’estrazione di campioni ordinati oppure di campioni non ordinati. Considerare campioni ordinati significa considerare diversi due campioni formati dagli stessi individui, però sorteggiati in ordine diverso (lotterie, gare sportive, ecc.). Ma questo vuol dire considerare diverse due distribuzioni in cui i contenitori hanno nel loro interno oggetti diversi, anche se in egual numero (si ricordi che il numero d’ordine in cui l’individuo viene sorteggiato equivale a dire che l’oggetto contrassegnato da quel numero d’ordine finisce nel contenitore corrispondente all’individuo sorteggiato).

Il principio di esclusione corrisponde invece alle modalità con cui viene fatto il sorteggio. Dire che un contenitore può contenere più di un oggetto corrisponde a dire che lo stesso individuo può comparire in più posti diversi, quindi può essere sorteggiato più di una volta nella costruzione del campione. L’estrazione allora viene fatta con reimbussolamento, vale a dire rimettendo il nome dell’estratto dentro l’urna. Se invece vale il principio d’esclusione un individuo non potrà comparire più di una volta nel campione: l’estrazione viene fatta senza reimbussolamento. L’ordine d’arrivo di una gara sportiva è un esempio classico di campione soggetto al principio d’esclusione, mentre non lo è una lotteria, perché la stessa persona può vincere anche più di un premio (al limite può vincerli tutti).

Quanto detto è sintetizzato nella tavola qui in basso, che probabilmente è utile presentare e illustrare agli studenti, prima di iniziare la meccanica statistica vera e propria. Si ha così il vantaggio di far familiarizzare gli studenti con i termini e con il linguaggio che saranno poi sistematicamente adoperati.

La tabella si legge in questo modo: la parte bianca centrale è la parte comune e contiene i quattro possibili modi di ripartire oggetti, o di formare campioni. Le parti grigie, superiore e inferiore, danno le due interpretazioni possibili. Quella superiore è il modello zanzara e illustra il caso in cui gli n oggetti vanno nei g contenitori. Si hanno i casi di oggetti distinguibili o non distinguibili, soggetti oppure no al principio d’esclusione. Quella inferiore è il modello mantide e illustra i possibili modi in cui si possono estrarre campioni di n elementi da una popolazione di numerosità g. Si hanno i casi di campioni ordinati o non ordinati, sorteggiati con reimbussolamento oppure no.

Bibliografia

1. John G. Kemeny, J. Laurie Snell, Gerald L. Thompson - Matematica e attività umane, vol. I, cap. 3; Feltrinelli, Milano, 1968 

2. Dario Palladino - Algebra, cap. 2; Editrice La Scuola, Brescia, 1995

2. Formula di Stirling

Non offre eccessive difficoltà, almeno se ci si limita all’approssimazione zero del logaritmo del fattoriale. L’identificazione di ln(n!) con l’area di un rettangoloide e la successiva approssimazione della stessa con un integrale conducono immediatamente al risultato. Magari si potrebbe fare anche qualche considerazione sul grado di approssimazione della formula e puntualizzare che l’errore assoluto che si commette usandola aumenta con l’aumentare di n mentre l’errore relativo diminuisce al crescere di n. 

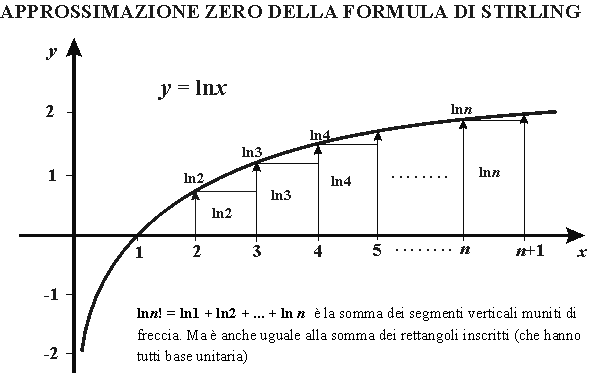
= area del rettangoloide inscritto

                                       (n<<1)

3. Massimi e minimi vincolati, metodo dei moltiplicatori di Lagrange

L’argomento è ancora abbordabile, anche se più complesso di quello precedente, se ci si limita a funzioni di due variabili con un solo vincolo e se gli studenti conoscono il metodo della rappresentazione delle funzioni di due variabili con le curve di livello nel piano xy. Certo, bisogna introdurre il gradiente, ma non si può avere tutto dalla vita. D’altronde i docenti di Scienze della Terra non possono che essere contenti di questo, loro che combattono tutto l’ultimo anno per far capire che cos’è un gradiente (di pressione, di temperatura, ecc.) e come si leggono le curve di livello.

Caso di una funzione di due variabili z=f(x,y) soggetta a un solo vincolo g(x,y)=0.

Rappresentazione della funzione z=f(x,y) col metodo delle curve di livello.

g(x,y) è una particolare curva di livello della funzione z=g(x,y).

c₁ < c₂ <c₃<c₄.

Supponiamo di voler cercare il massimo della f(x,y) soggetta alla condizione g(x,y)=0. Partendo dal punto A, e percorrendo la curva g(x,y)=0 verso B, si vede che la curva è intersecata dalle curve di livello della z=f(x,y) corrispondenti a valori della funzione sempre più elevati: f(x,y) cresce andando da A verso B. Oltrepassato B si vede che il valore della funzione diminuisce. In B si ha il massimo condizionato:

f(x_B,y_B) = max = c₃

Le due linee di livello f(x,y)=c₃ e g(x,y)=0 hanno in B la stessa tangente. Quindi i gradienti delle due funzioni z=f(x,y) e z=g(x,y) hanno in B la stessa direzione, sono cioè uno multiplo dell’altro

                  [grad f = l grad g]

Passando alle componenti:

L’estensione alle funzioni di più di due variabili e/o al caso di più vincoli è immediata.