Talete misura la piramide

In terra d’Egitto, Talete sbalordisce tutti, agrimensori, sacerdoti e il re: misura la piramide, la tomba del re. Il successo è pieno e totale e Plutarco così lo riporta: " [Il re] è rimasto singolarmente ben impressionato dal modo in cui hai misurato la piramide, [...], limitandoti a collocare il tuo bastone al limite dell’ombra proiettata dalla piramide stessa; formatisi, al contatto col sole, due triangoli, dimostrasti che la proporzione esistente fra la lunghezza del bastone e l’altezza della piramide era la stessa che intercorreva fra la lunghezza delle due ombre. 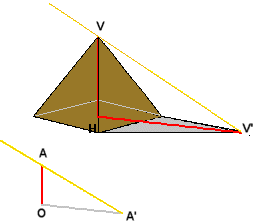Ciò nonostante .... ti si muove l’accusa d’avere in odio i re".

Poiché i raggi del sole sono paralleli, i triangoli AOA' e VHV' sono simili e, come l'ombra del bastone è doppia della sua altezza, così l'ombra della piramide sarà doppia rispetto alla sua altezza.

E' questa un'importante applicazione del teorema di Talete: la sua formulazione è forse nata dall'osservazione dei raggi del sole. Questi, incontrando i corpi materiali, vengono fermati, e si formano delle ombre.

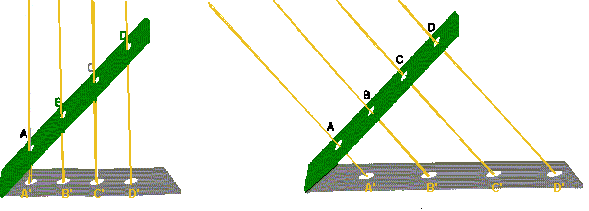
immagine tratta da "Castelnuovo Gori Valenti - Matematica oggi 2" edizione La Nuova Italia

Osservando tali ombre si può notare che nel corso della giornata queste variano ma, pur variando, si nota che qualcosa rimane immutato:

i segmenti AB e BC, che sono uguali, si trasformano nei segmenti A'B' e C'D' che restano sempre uguali fra di loro;
AC = 2AB, si trasforma in A'C' = 2AC, ossia il rapporto fra segmenti corrispondenti non muta.

Il formare segmenti proporzionali su due trasversali è caratteristico delle rette parallele, come abbiamo verificato attraverso un interessante esperimento di fisica