| Un esempio di equazione | |||||||||||||
| Radice: soluzione di un'equazione, che all'inizio è nascosta come la ridice di un albero. Indica anche la radice quadrata di un numero: anche in questo caso occorre estrarre il numero dal suo... nascondiglio! |
I quadrati e le radici sono uguali a un numero:
al- Khuwarizmi afferma: "La soluzione è:
Seguiamo il ragionamento passo per passo, usando le
notazioni moderne.
Scriviamo la formula in forma equivalente, avvicinandoci però al tipo di risoluzione che viene data dal matematico arabo:
Come si vede, il procedimento indicato da al- Khuwarizmi
è proprio, con le distinzioni che abbiamo fatte, il nostro. |
|
|||||||||||
|
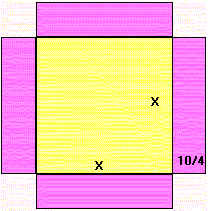
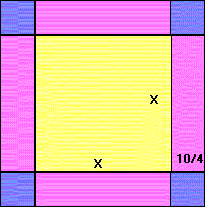
Dimostrazione geometrica Si costruisce il quadrato di lato x
Sui suoi lati si costruiscono 4 rettangoli che hanno la seconda dimensione uguale a 10/4
La figura così ottenuta ha area x2+10x, quindi, in base a quello che sappiamo, l'area è 39. Si completa poi la figura con quattro quadratini di lato 10/4
Si ottiene così un quadrato di area 39+4*100/16=64, il cui lato misura 8. Si deduce quindi x = 8-10/2=8-5=3.
|
|||||||||||||

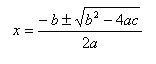
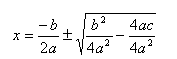
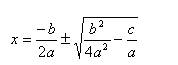
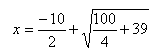 ed
infine
ed
infine