
Due palline sono ferme in ciascuno dei fuochi dell'ellisse. Se si fa partire una delle due da uno dei fuochi, lanciandola in qualunque direzione, dopo aver toccato la sponda, urterà l’altra pallina situata nell'altro fuoco.
 |
Ellissografo di Cardano
Fissate al piano, rappresentato dalla base di legno, ci sono due scanalature perpendicolari lungo le quali scorrono due cursori a cui sono incernierate due guide scorrevoli sull’asta. Ad
un’estremità dell’asta è fissata una punta scrivente. Facendo
scorrere i cursori nelle rispettive scanalature il punto C descrive
un’ellisse. |
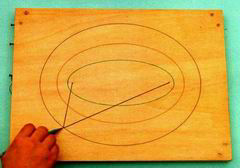 |
Strumento
a filo per ellisse
Nel piano di legno, in due punti, corrispondenti ai fuochi dell’ellisse, ci sono due chiodi, attaccato ai quali passa un filo di lunghezza maggiore della distanza tra i due punti.La punta scrivente che mantiene il filo teso descrive sul piano un’ellisse con semiasse maggiore pari alla metà della lunghezza del filo. |
 |
Strumento
a filo per
parabola
Questo modellino è costituito da un’asta scorrevole lungo una guida rettilinea e da un filo fissato per un estremo all’asta e per l’altro estremo ad un punto del piano che corrisponderà al fuoco della parabola. Prendiamo una punta scrivente in modo che mantenga teso il filo rimanendo appoggiata all’asta. Se si fa scorrere l’asta lungo la guida rettilinea, la punta scrivente descriverà una parabola. |
 |
Strumento
a filo per
Iperbole
Un’asta
può ruotare attorno ad un perno fissato nel piano di legno (questo punto
sarà un fuoco dell’iperbole). Un
filo di lunghezza minore della lunghezza dell’asta è teso tra
l’estremo libero dell’asta ed il punto fissato nel piano che
corrisponderà all’altro fuoco dell’iperbole. Quando
l’asta ruota attorno al perno una punta scrivente, che mantiene il filo
teso e che rimane sempre appoggiata all’asta, descrive un arco di
iperbole. |
 |
Conicografi: ellisse
Questo modello è costituito da un’asta e da un rombo articolato. L’asta ruota attorno ad un suo estremo fissato nel piano e trascina con sé il rombo. Facendo ruotare il sistema la punta scrivente descrive un’ellisse.
|
 |
Conicografi: parabola
Questo
sistema articolato permette di tracciare una parabola. Un’asta scorrendo tra due guide rettilinee parallele, trascina con sé un rombo articolato. Questo
movimento fa si che la punta scrivente descriva una parabola.
|
 |
Conicografi:
iperbole
È costituito da un rombo articolato e da un’asta che può ruotare attorno ad un suo estremo, trascinando con sé il rombo poichè sono incernierati in un punto. Se si ruota il sistema una punta scrivente descriverà un’iperbole. |