Conoscenze di geometria attribuite a Talete

• Gli angoli alla base di un triangolo isoscele sono uguali;
• Il cerchio è bisecato da ogni diametro;
• Ogni triangolo inscritto in una semicirconferenza è rettangolo;
• Un fascio di rette parallele individua su due trasversali due classi di grandezze direttamente proporzionali

Probabilmente, nel periodo in cui visse Talete, la geometria, come quella di tutte le popolazioni antiche, era una geometria che si basava su ipotesi non dimostrabili: la geometria che oggi chiamiamo intuitiva. Non dobbiamo sottovalutare l'importanza dell'intuizione, infatti, per individuare le proprietà sopraenunciate, è necessario un grande sforzo di astrazione e buona capacità di distinguere ciò che varia da ciò che non varia: ad esempio, nel caso del triangolo isoscele, l'angolo al vertice varia, mentre il vertice si allontana dalla base, come pure variano gli angoli alla base, tuttavia, pur variando, essi si mantengono sempre uguali fra loro.
Notiamo poi espressamente che le proprietà delle figure geometriche attribuite a Talete sono caratteristiche degli enti alle quali esse si riferiscono. Facciamo un esempio:

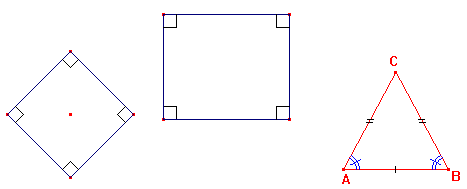Se un triangolo è isoscele, allora ha gli angoli alla base uguali, e viceversa, se un triangolo ha gli angoli alla base uguali, allora è isoscele.
Diciamo perciò che avere gli angoli alla base uguali è condizione necessaria e sufficiente per essere un triangolo isoscele.
Nel caso dei quadrilateri, invece, possiamo dire: se un quadrilatero è un quadrato, allora ha tutti gli angoli  uguali ma il viceversa non è vero, infatti esistono quadrilateri che hanno gli angoli uguali senza essere quadrati.