| SITO LICEO | PAGINA INIZIALE | LETTERATURA |
NUMERI MAGICI - NUMERI MEMORABILI |
||
| SOPRAVVIVENZE | BIBLIOGRAFIA | ||||
|
IL NUMERO DIECI |
|||||
Si dice sezione aurea del segmento AB,
il segmento AC, con C compreso tra A e B, medio proporzionale tra l'intero
segmento AB e la parte rimanente CB.
In altri termini
AB : AC = AC : CB
Se AB misura a, per trovare la misura di AC basta impostare la
proporzione a: x = x : (a - x) da cui si ricava x2 = a(a-x)
e quindi si ottiene l'equazione di secondo grado x2 + ax -a2
= 0
Risolvendo l'equazione, e scartando la radice negativa, si ottiene x
≈ 0.618a
La sezione aurea è un rapporto di numeri molto particolare, che incontriamo ovunque, nella natura
e nell'arte e che ci risulta particolarmente gradito alla vista per la sua
inconfondibile armonia.

La sezione aurea fu studiata dai Pitagorici i quali, scoperto che il lato del decagono regolare inscritto in una circonferenza di raggio r è la sezione aurea del raggio, costruirono anche il pentagono regolare intrecciato o stellato, o stella a 5 punte ( il pentagramma (dal greco pente, "cinque" e gramma, "linea") ottenendolo dal decagono regolare mediante la congiunzione di un vertice si e uno no.
Notiamo innanzitutto una proprietà del pentagono regolare inscritto in una circonferenza:
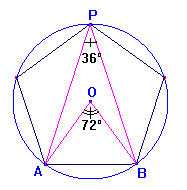
L'angolo al centro AÔB è di 72° (360° : 5), e dunque l'angolo alla
circonferenza APB è di 36°, infatti l'angolo alla circonferenza è metà
dell'angolo al centro corrispondente. Allora siamo di fronte,
di nuovo, ad un triangolo isoscele (ABP) con l'angolo
al vertice di 36°. Allora nel pentagramma le diagonali si incontrano secondo
un rapporto aureo.
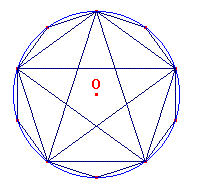
I Pitagorici usavano il pentagramma, come nella figura che segue, con due
punte verso l'alto:
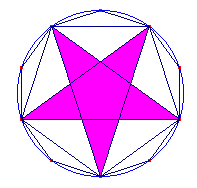
Si può notare che il pentagramma, che è un esempio di poligono regolare
non-convesso, si può anche ottenere prolungando i lati di
un pentagono regolare: se poi si tracciano le diagonali di tale pentagono si
ottiene nuovamente un pentagramma... intrigante, non c'è che dire!
A questa figura è stata attribuita per
millenni à un’importanza misteriosa probabilmente per la sua proprietà di
generare la sezione aurea, da cui è nata .
DERIVA DA
latino decem
ALCUNE PROPRIETA' MATEMATICHE
E' la base del nostro sistema di numerazione, molto probabilmente dovuto all'abitudine di contare con le dita.
E' l'unico numero triangolare che sia la somma di due quadrati dispari (10 = 12 + 32) e l'unico intero composto i cui divisori interi, a parte 1, siano della forma x2 + 1 (2 = 12 + 1, 5 = 22 + 1, 10 = 32 + 1).
Un numero è divisibile per 10 se termina per 0.
|
|
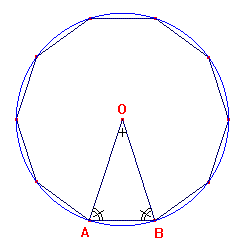
Teorema Dimostrazione Sia AB il
lato del decagono regolare inscritto nella circonferenza di centro O;
vogliamo dimostrare che AB è la parte aurea del raggio OB. |
|
|
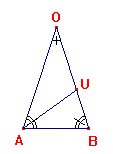
Tracciamo la bisettrice AU dell’angolo OÂB:
questa divide l'angolo OÂB in due angoli di 36°. Di conseguenza l'angolo AÛB misura 72° e quindi il triangolo AUB, avendo due angoli uguali, è isoscele e AB = AU. Anche il triangolo AOU è isoscele avendo gli angoli i OÂU e Ô di 36° per cui AU = OU. Dunque AB = AU = OU. |
|
I triangolo isosceli AUB e AOB sono simili
per il primo criterio di similitudine, infatti hanno tutti gli angoli
rispettivamente uguali, e quindi Se il
cerchio ha raggio r, il lato l del decagono regolare inscritto
vale
|
|
CURIOSITA'
Era sacro ai pitagorici
ASSOCIAZIONI
I
comandamenti della legge ebraica consegnati da Dio a Mosè (Decalogo).
Le dita delle mani e dei piedi degli antropomorfi.
La base della nostra numerazione.
Il numero sulla maglia del centravanti di una squadra di calcio
Le piaghe d'Egitto (1: l'acqua del Nilo rosseggia di sangue; 2: le rane
pullulano dal Nilo e invadono le case; 3: zanzare e 4: mosconi diventano un
tormento insopportabile; 5: il bestiame è vittima di una pestilenza; 6:
epidemia di ulceri con eruzioni pustolose attacca uomini e animali; 7: la
grandine rovina le colture di lino e di orzo; 8: le cavallette divorano
tutto quanto è stato risparmiato dalla grandine; 9: le tenebre offuscano il
sole per 3 giorni; 10: un malore misterioso fa morire i primogeniti
Egiziani).
ALCUNI
VOCABOLI CORRELATI AL NUMERO 10
Decimo, decano, deca, decina, decenne, decennale, decagono, dicembre
(dall'antico calendario romano che iniziava a marzo e indicava così il
decimo mese)
AFORISMI
Nunc autem sciendum, quod Deus dando
legem Moysi, dedit decem praecepta in duabus tabulis lapideis scripta:
quorum tria in prima tabula scripta pertinent ad amorem Dei; septem vero
scripta in secunda tabula pertinent ad amorem proximi. - Corpo
tomistico - Tommaso d'Aquino
Decem oves faciunt gregem,
Quinque boves faciunt armentum,
Tres canonici faciunt chorum,
Et ratio est quia, quo maior est bestia eo minor requiritur numerus.
(Dieci pecore fanno un gregge,
cinque buoi fanno un armento,
tre canonici fanno un coro.
E la ragione è che, quanto più sono bestie, tanto meno ce ne vogliono.) (dal
Forum dei Cattolici Romani)
SITO LICEO | PAGINA INIZIALE | MAPPA | MITO | LETTERATURA | EPICA | MATEMATICA | SOPRAVVIVENZE| BIBLIOGRAFIA | AUTORI