| SITO LICEO | PAGINA INIZIALE | LETTERATURA |
NUMERI MAGICI - NUMERI MEMORABILI |
||
| SOPRAVVIVENZE | BIBLIOGRAFIA | ||||
|
IL NUMERO NOVE |
|||||
Esempi di prova del nove
|
34 × 26 = |
Somma delle cifre
del 1° fattore: 3 + 4 = 7 |
Somma delle cifre
del 2° fattore: 2 + 6 = 8 |
| Somma
delle cifre del prodotto: 8 + 8 + 4 = 20 2 + 0 = 2 |
Somma delle cifre
del prodotto dei due numeri in alto: 7 × 8 = 56 5 + 6 = 11 1 + 1 = 2 |
|
| 884 | 2 = 2 → la prova è riuscita | |
|
34
+ 26 = |
Somma delle cifre
del 1° addendo: 3 + 4 = 7 |
Somma delle cifre
del 2° addendo: 2 + 6 = 8 |
| Somma
delle cifre della somma: 6 + 0 = 6 |
Somma delle cifre
della somma dei due numeri in alto: 7 + 8 = 15 5 + 1 = 6 |
|
| 60 | 6 = 6 → la prova è riuscita | |
| 628 : 17 = | Somma delle cifre
del divisore: 1 + 7 = 8 |
Somma delle cifre
del quoziente: 3 + 6 = 9 -> 0 |
| Somma delle cifre
del prodotto dei due numeri in alto + somma delle cifre del resto: 8 × 0 = 0 1 + 6 =7 0 + 7 = 7 |
Somma delle cifre
del dividendo: 6 + 2 + 8 = 16 1 + 6 = 7 |
|
| quoziente 36, resto 16 | 7 = 7 → la prova è riuscita | |
|
34
× 26 = |
Somma delle cifre
del 1° fattore: 3 + 4 = 7 |
Somma delle cifre
del 2° fattore: 2 + 6 = 8 |
| Somma
delle cifre del prodotto: 8 + 4 + 8 = 20 2 + 0 = 2 |
Somma delle cifre
del prodotto dei due numeri in alto: 7 × 8 = 56 5 + 6 = 11 1 + 1 = 2 |
|
| 848 | 2 = 2 → la prova è riuscita, ma in realtà il prodotto è 884 | |
DERIVA DA
latino novem
ALCUNE PROPRIETA' MATEMATICHE
É
un numero quadrato (32 = 9) e
quindi la somma di due numeri triangolari
consecutivi (3 + 6 = 9).
I primi nove numeri possono essere disposti in un
quadrato magico di ordine tre.
E' il quarto numero fortunato.
Un numero è divisibile solo per 9 se e solo se lo è la somma delle sue
cifre, ed anzi, per trovare il resto resto nella divisione per 9 di un
numero, basta sommare le cifre del numero e ripetere il procedimento fino a
quando si ottiene una sola cifra: se la cifra è 9 il resto è 0, altrimenti
il resto è la cifra trovata.
Esempi:
Dato 341 si ha: 3 + 4 + 1 = 8. Dunque il resto della divisione di 343 per 9 è 8.
Dato 3458 si ha: 3 + 4 + 5 + 8 = 20; 2 + 0 = 2. Dunque il resto della divisione di 3458 per 9 è 2.
Dato 342 si ha: 3 + 4 + 2 = 9. Dunque il resto della divisione di 342 per 9 è 0.
Prova del nove
Fu
introdotta da Leonardo Pisano, detto il Fibonacci, nel suo
Liber Abaci
nel 1202. Quindi in Europa fu importata dagli Arabi, ma molto probabilmente
fu un'invenzione degli indiani.
Sostituire ad ogni numero il suo resto rispetto alla divisione per 9
equivale ad operare nell'aritmetica modulo 9.
E' poi facile verificare che, se ad esempio addizioniamo vari numeri, e
dividiamo la somma per 9, il resto è uguale alla somma dei resti dei singoli
addendi sempre nella divisione per 9, anche se questa proprietà è valida per
qualsiasi modulo. Ad esempio:
Una
circonferenza per 9 punti
Nel triangolo ABC:
CURIOSITA' NEL
PASSATO Gli antichi Romani festeggiavano per nove
giorni un evento prodigioso, e nove giorni durava il lutto per i morti.
ASSOCIAZIONI I pianeti del sistema solare;
HANNO DETTO
Novem figurae indorum he sunt 9 8 7 6
5 4 3 2 1 Cum his itaque novem figuris, et cum hoc signo 0, quod arabice
zephirum appellatur, scribitur quilibet numerus, ut inferius demonstratur.
(Leonardo Fibonacci, Liber
abaci, inizio del primo capitolo)
Si tratta di un controllo per vedere se il risultato di un'operazione è
corretto secondo gli schemi riportati a sinistra nella pagina. Iniziamo
dalla moltiplicazione.
Come si può osservare, si costruisce una tabella in cui si pongono le somme
delle cifre dei vari numeri, secondo la regola riportata nelle rispettive
celle, fino ad ottenere una sola cifra, (se si ottiene 9 la cifra viene
sostituita da 0). In altri termini, si sostituisce ad ogni numero il suo
resto rispetto nella divisione per 9.
NOTA BENE Se il risultato della moltiplicazione, anziché quello giusto
884, fosse stato 848, la prova del 9 avrebbe funzionato ugualmente.
Conclusione: se la
prova del 9 è scorretta allora il risultato è certamente sbagliato; se la
prova del 9 è corretta, allora non possiamo essere sicuri che il risultato
sia quello giusto, anche se
abbiamo aumentato la probabilità che lo sia.
(Anche nei linguaggi di programmazione
 l'operazione
a mod b equivale a trovare il resto della divisione di a : b)
l'operazione
a mod b equivale a trovare il resto della divisione di a : b)
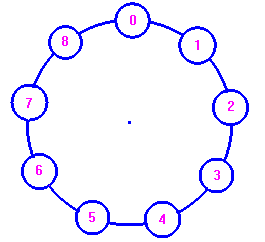
Un
esempio concreto di aritmetica modulare è fornito dall'orologio analogico,
in cui le ore sono numerate da 1 a 12 (ma noi a 12 sostituiamo lo 0). In
questo caso, se sono le 8, fra 6 ore saranno le 2. In altri termini si
effettua la somma non più spostandosi verso destra su una semiretta
orientata, ma spostandosi, in verso orario, sull'orologio. (Nell'immagine a
sinistra è presentato un orologio con 9 ore, che funziona come quello
usuale solo che in questo caso, ad esempio, 8 + 6 = 5)
Lavorare in modulo 9 è particolarmente semplice visto
che il resto della divisione per 9 di un numero si ottiene semplicemente
addizionando le cifre del numero.
(234 + 46 + 25) mod 9 = 305 mod 9 = 8
234 mod 9 + 46 mod 9 + 25 mod 9 = 0 + 1 + 7= 8
Analogamente: (34 × 26) mod 9 = 884 mod 9 = 2 e (34 mod
9) × (26 mod 9) = (7 × 8) mod 9 = 2
Ecco che la prova del 9 acquista un nuovo significato.
approfondimento su
Base cinque

H, K ed
I sono i piedi delle altezze;
O è l'ortocentro;
L, M ed
N sono i punti medi dei lati;
P, Q ed
R sono i punti medi rispettivamente dei segmenti AO, BO e CO.
Per ogni triangolo esiste sempre una circonferenza che passa per questi 9
punti, nota come circonferenza di Feuerbach (Karl Wilhelm, matematico
tedesco, 1800, 1834)
Ad Allah sono attribuiti novantanove nomi.
Nel Medioevo ai gatti erano attribuite 9 vite.
Nove erano gli scalini che portavano al trono cinese.
le muse figlie di Zeus protettrici delle arti e delle scienze;
i gironi dell’Inferno e i cieli che fanno corona all'Emisfero nella Divina
Commedia di Dante Alighieri.
ALCUNI
VOCABOLI CORRELATI AL NUMERO 9
Nono, novembre (dall'antico calendario romano che iniziava a marzo e
indicava così il nono mese), novena (periodo di nove giorni dedicato alla
preghiera), novenne (9 anni di età).
Ci sono nove figure degli
indiani: 9 8 7 6 5 4 3 2 1. Con queste nove figure, e con il simbolo 0, che
gli arabi chiamano zefiro, qualsiasi numero può essere scritto, come
dimostreremo.
SITO LICEO | PAGINA INIZIALE | MAPPA | MITO | LETTERATURA | EPICA | MATEMATICA | SOPRAVVIVENZE| BIBLIOGRAFIA | AUTORI