SITO LICEO PAGINA INIZIALE

MAPPA

MITO

 LETTERATURA

NUMERI MAGICI - NUMERI MEMORABILI

EPICA

MATEMATICA

 SOPRAVVIVENZE BIBLIOGRAFIA

GLI AUTORI
 

NUMERI QUADRATI

Quadrati perfetti razionali

Sono numeri razionali non negativi esprimibili come frazione che, ridotta ai minimi termini, ha sia come numeratore che come denominatore (diverso da zero), un quadrato perfetto.
Ad esempio 20,25 = 81/4 = 92/22
Le radici quadrate di tutti i numeri razionali non negativi che non sono quadrati perfetti sono numeri irrazionali, cioè non sono esprimibili sotto forma di frazione.

Somma di quadrati, differenza di quadrati

La somma di quadrati a2 + b2  non è scomponibile; la differenza di quadrati a2 - b2 = (a + b)(a - b)

Esempio geometrico

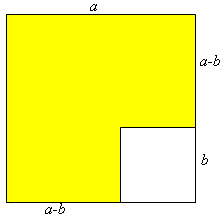
Se al quadrato di lato a sottraiamo il quadrato di lato b (con a > b) otteniamo il poligono concavo in giallo che ha area
a(a - b) + b(a - b) = (a + b)(a - b)

Programma per i numeri quadrati

Abbiamo preparato un programma in Visual Basic che disegna, a scelta, i primi dieci numeri quadrati

  • o come somma di dispari consecutivi

  • o come composizione di numeri triangolari

Per scaricare il programma CLICCA QUI

 

 

I Pitagorici rappresentavano alcuni numeri in schemi composti da punti e classificavano i punti in base alla forma dello schema che ottenevano. Un numero m è un quadrato perfetto se e solo se è possibile disporre m punti a formare un quadrato, per questo l'elevamento alla seconda potenza è chiamato anche elevamento al quadrato.
I numeri nella figura sono detti quadrati perché  è possibile disporre le unità che li compongono su una griglia regolare, in modo da formare un quadrato.
Nella figura si vede anche come un numero quadrato sia la somma di due numeri triangolari.

DIMOSTRAZIONE

 
n -simo numero triangolare
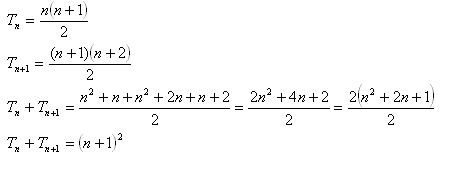numero triangolare successivo 
somma dei due numeri
conclusione


Un' altra proprietà dei numeri quadrati è di poter essere espressi come somma di  numeri dispari consecutivi, come si vede dalla figura che segue.

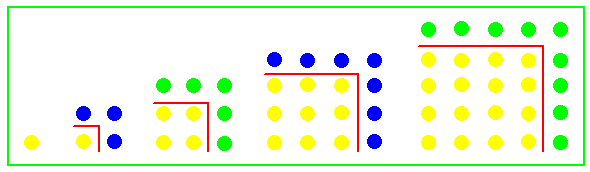
DIMOSTRAZIONE

Calcoliamo infatti la differenza di due quadrati consecutivi (n è un numero naturale):

(n+1)2 - n2 = n2 + 2n + 1 - n2 = 2n + 1

Si vede che si ottiene un numero dispari, e facendo variare n nell'insieme dei numeri naturali si ottiene la successione dei numeri dispari.
Ad esempio:

Si ha e viceversa

12 - 02 = 1

22 - 12 = 4 - 1 = 3

32 - 22 = 9 - 4 = 5

42 - 32 = 16 - 9 = 7

... e così via.

12  = 1

22  = 1 + 3

32  = 1 + 3 +  5

42  = 1 + 3 + 5 + 7

... e così via.

L' n-simo numero quadrato sarà la somma dei primi n numeri dispari.

 

     SITO LICEO | PAGINA INIZIALE | MAPPA | MITO | LETTERATURA | EPICA | MATEMATICA | SOPRAVVIVENZE| BIBLIOGRAFIA | AUTORI