| SITO LICEO | PAGINA INIZIALE | LETTERATURA |
NUMERI MAGICI - NUMERI MEMORABILI |
||
| SOPRAVVIVENZE | BIBLIOGRAFIA | ||||
|
IL NUMERO QUATTRO |
|||||
|
|
Il problema dei quattro colori

Data una qualsiasi mappa piana, se ne colorino le regioni seguendo i seguenti criteri:
-
ogni regione ha colore diverso dalle confinanti;
-
si deve usare il minimo possibile di colori.
Se rappresentiamo ogni regione con un punto ed uniamo solo i punti corrispondenti a regioni confinanti possiamo trasformare la mappa in un grafo planare (che cioè appartenga ad un piano e non abbia spigoli che si intersecano), come nella figura che segue:
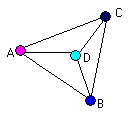
Allora il problema può essere così
trasformato: quanti colori, al massimo, possono essere utilizzati per
colorare i vertici adiacenti di un grafo planare?
Nella figura in alto occorrono almeno quattro colori, e nessuno è riuscito a
trovare una mappa ( o un grafo) per i quali siano serviti più di quattro
colori.
Si dice, in breve, che un grafo planare è 4 - colorabile.
La storia del problema dei quattro
colori è abbastanza incerta: alcuni affermano che il primo a porsi il
problema, nell’ottobre 1852, fu Francis
Guthrie, un giovane matematico dell’University College di Londra, mentre
stava colorando una cartina delle contee dell’Inghilterra; altri riportano
un problema posto da Möbius nel 1840 ai suoi studenti:
"Un re dell'India con un grande regno aveva cinque figli. Nelle sue
volontà decretò che dopo la sua morte il regno dovesse essere diviso in
cinque parti in modo che ogni territorio avesse un lato (e non un punto)
in comune coi rimanenti. Come venne diviso il regno?"
Möbius sosteneva che il problema non avesse soluzione.
Il problema non è stato dimostrato in modo del tutto soddisfacente, infatti è stato risolto con un algoritmo informatico e per analizzare tutti i casi possibili i computer impiegarono circa 1200 ore e servirono più di 500 pagine per trascrivere a mano tutte le verifiche che costituivano la dimostrazione.
Approfondimento su matematicamente.it con un articolo di Anita Pasotti.
DERIVA DA
latino quottuor
ALCUNE PROPRIETA' MATEMATICHE
É il secondo numero quadrato.
E' il numero più piccolo che può essere scritto come somma di numeri primi: 4 = 2 + 2
Un numero è divisibile per quattro le lo è il numero composto dalle sue due ultime cifre.
Il più semplice solido platonico, il tetraedro, ha 4 vertici e 4 spigoli.
Ogni numero naturale è la somma di al massimo 4 quadrati.
Partendo da un numero intero diverso da
zero, si
formi la sequenza formata dalla somma dei quadrati delle sue cifre.
Si ripeta il procedimento. Si presentano due casi:
si arriva ad 1 ed il ciclo termina
623 - 49 - 97 - 130 - 10 - 1
si arriva ad un ciclo nel quale 4 è il numero più piccolo.
725 - 78 - 113 - 111 - 2 - 4...
... 4 - 16 - 37 -58 - 89 - 145 - 42 - 20 - 4...
PROVA ALTRI NUMERI CON IL NOSTRO PROGRAMMA!
Per il problema dei quattro colori abbiamo preparato una scheda a sinistra nella pagina.
CURIOSITA'
I
pitagorici chiamavano i numeri divisibili per quattro pari - pari. Per
questo motivo il quattro era associato alla Giustizia.
Per i Maya i “momenti creativi” erano quattro; quattro le ere mitiche che,
per i peruviani, avrebbero preceduto la creazione dell’uomo. Per l’induismo
ci troviamo nell’ultimo periodo, il Kaliyuga, in
cui le condizioni generali e morali del mondo raggiungono il punto più
basso, in attesa del prossimo periodo che riprenderà con un’età felice.
ASSOCIAZIONI
Le stagioni (inverno, primavera, estate, autunno)
I punti cardinali
I cavalieri dell'Apocalisse
Nel Vecchio Testamento erano quattro i fiumi del Paradiso, uno per ciascuna
direzione, a prefigurare i quattro Vangeli del Nuovo Testamento.
Le dimensioni dello spazio - tempo di Einstein.
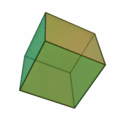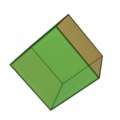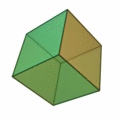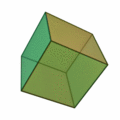
Gli elementi naturali di Aristotele: terra, il cui simbolo
era il cubo, l'aria, il cui simbolo era l'ottaedro, l'acqua, il cui simbolo
era il dodecaedro, il fuoco, il cui simbolo era l'icosaedro.
|
Cubo |
Ottaedro |
Dodecaedro |
Icosaedro |
|
|
|
|
 |
|
|
|||
ALCUNI
VOCABOLI CORRELATI AL NUMERO
4
Quarto; quarta (in musica, il quarto grado della scala diatonica);
quartetto, quartina; quaternario; quartana (febbre ogni 4 giorni);
quartiere; quartirolo; quartogenito; quadriglia; quadrivio ...
AFORISMA
Quattuor abscondi non possunt: tussis,
amor, ignis, dolor. (Anonimo)
Quattro cose non si possono nascondere: la tosse, l'amore, il fuoco e il
dolore.
SITO LICEO | PAGINA INIZIALE | MAPPA | MITO | LETTERATURA | EPICA | MATEMATICA | SOPRAVVIVENZE| BIBLIOGRAFIA | AUTORI