SITO LICEO PAGINA INIZIALE

MAPPA

MITO

 LETTERATURA

NUMERI MAGICI - NUMERI MEMORABILI

EPICA

MATEMATICA

 SOPRAVVIVENZE BIBLIOGRAFIA

GLI AUTORI
 

NUMERI TRIANGOLARI

Test per i numeri triangolari

Per stabilire se un numero naturale n è triangolare basta calcolare

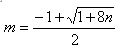
Se m è intero allora n è triangolare, altrimenti non lo è.

Infatti, se n è un numero triangolare, esiste un numero naturale m tale che

Svolgendo i calcoli  si ottiene l'equazione di secondo grado m2 + m - 2n = 0
La formula non è altro che l'eventuale  soluzione positiva dell'equazione.

Un programma per i numeri triangolari

Abbiamo preparato un programma in Visual Basic che:

  • disegna, a scelta, i primi dieci numeri triangolari

  • calcola l'n- simo numero triangolare inserendo n

  • stabilisce se un numero è triangolare

Per scaricare il programma CLICCA QUI

 

 

 

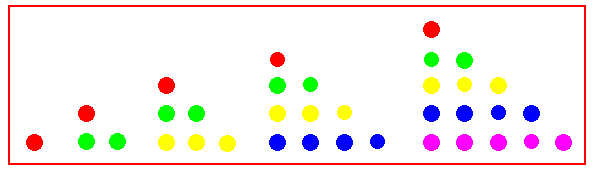
I Pitagorici rappresentavano alcuni numeri in schemi composti da punti e classificavano i punti in base alla forma dello schema che ottenevano.
I numeri in figura sono detti triangolari perché  è possibile disporre le unità che li compongono su una griglia regolare, in modo da formare un triangolo rettangolo isoscele. (Ma sarebbe possibile disporli anche in modo da formare un triangolo equilatero)

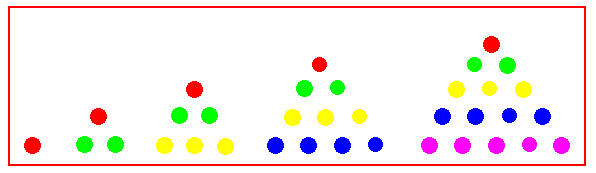
Lo schema è così costruito:

  1. si pone 1 oggetto (nel nostro caso un cerchietto) sulla prima riga,

  2. si pongono 2 oggetti sulla seconda riga,

  3. e così via

Come trovare l'n-simo numero triangolare?

  • Il primo numero triangolare = 1

  • Il secondo numero triangolare = 1 + 2 = 3

  • Il terzo numero triangolare = 1 + 2 + 3 = 6

  • Il quarto numero triangolare = 1 + 2 + 3 + 4  = 10

  • ...

L'n -simo numero triangolare è perciò sempre la somma dei primi n numeri naturali, a partire da 1 e quindi la formula
n(n + 1) :2 dà luogo ai numeri triangolari. Una verifica della formula è rappresentata nelle figure che seguono

 

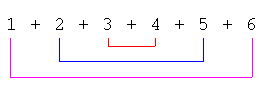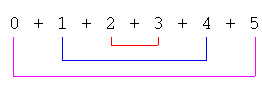Se n = 6 abbiamo 3 coppie, ciascuna di somma 7,
e quindi la somma dei numeri è 21. In lettere:
(n :2)(n + 1)		 Se n = 5, cioè dispari, aggiungendo lo 0, otteniamo 3 coppie, ciascuna di somma 5,  e quindi la somma dei numeri è 15. In lettere: [(n + 1) :2]n

 SITO LICEO | PAGINA INIZIALE | MAPPA | MITO | LETTERATURA | EPICA | MATEMATICA | SOPRAVVIVENZE| BIBLIOGRAFIA | AUTORI