SITO LICEO PAGINA INIZIALE

MAPPA

MITO

 LETTERATURA

NUMERI MAGICI - NUMERI MEMORABILI

EPICA

MATEMATICA

 SOPRAVVIVENZE BIBLIOGRAFIA

GLI AUTORI
 

I NUMERI NELLA SCUOLA PITAGORICA

Si parla in genere di scuola pitagorica piuttosto che di Pitagora in quanto la sua figura resta avvolta nella leggenda: originario di Samo, visse probabilmente nel VI/V secolo a.C. in Italia, dove fondò la sua scuola nei pressi di Crotone; i suoi seguaci avevano una vera e propria venerazione per la sua persona e le sue parole ma di lui non ci è pervenuto alcuno scritto.

La rappresentazione, mediante un triangolo equilatero di lato quattro, della sacra tetraktys.
Il riferimento al triangolo è importante perché sembra indicare che presso i Greci i numeri fossero rappresentati per mezzo di punti.
La tetraktys ha un valore rappresentativo -simbolico, in quanto ogni punto di questo particolare triangolo viene a rappresentare le relazioni tra le seguenti forme della geometria: l’1 indica il punto, il 2 la linea, il 3 la superficie piana, il 4 il solido.

La crisi della filosofia pitagorica

E' da ricercarsi nella scoperta degli irrazionali, numeri che non possono essere scritti sotto forma di frazione, e dunque come rapporto di due interi.
Una bella lezione sull'argomento è a questo link: Progetto Polymath. 

Come riferisce Aristotele, (Met, libro A), i pitagorici ritennero "che tutto quanto l'universo fosse armonia e numero".

... Fu proprio una intuizione musicale che permise a Pitagora di formulare quel legame fra matematica e natura che costituisce, probabilmente, la scoperta più profonda e feconda della storia dell'intero pensiero umano. Secondo Giamblico, l’episodio è il seguente.
Un giorno Pitagora passò di fronte all'officina di un fabbro, e si accorse che il suono dei martelli sulle incudini era a volte consonante, e a volte dissonante. Incuriosito, entrò nell'officina, si fece mostrare i martelli, e scoprì che quelli che risuonavano in consonanza avevano un preciso rapporto di peso. Ad esempio, se uno dei martelli pesava il doppio dell'altro, essi producevano suoni distanti un'ottava. Se invece uno dei martelli pesava una volta e mezzo l'altro, essi producevano suoni distanti una quinta (l'intervallo fra il do e il sol). Tornato a casa, Pitagora fece alcuni esperimenti con nervi di bue in tensione, per vedere se qualche regola analoga valesse per i suoni generati da strumenti a corda, quali la lira. Sorprendentemente, la regola era addirittura la stessa! Ad esempio, se una delle corde aveva lunghezza doppia dell'altra, esse producevano suoni distanti un'ottava. Se invece una delle corde era lunga una volta e mezzo l'altra, esse producevano suoni distanti una quinta...
[da Pitagora,: la Matematica dell'armonia di Piergiorgio Odifreddi (La Stampa giovedì 7 maggio 1998)]

I Pitagorici ritennero i numeri il principio di tutto anche perché constatarono che il mondo non è un caos, disordinato, ma una armonia misurabile attraverso i numeri.
Occorre precisare che i Pitagorici consideravano "numeri" solo gli interi positivi (i numeri naturali) e al più di questi si potevano considerare i rapporti (i numeri razionali).
I numeri hanno un principio: il pari e il dispari, fattori primordiali, da cui scaturiscono i numeri, a loro volta origine di tutte le cose. I numeri poi avevano una loro personalità: i numeri dispari erano indissolubili, maschili, perfetti e benevoli; i numeri pari erano invece scindibili e dunque femminili, imperfetti e doppi.
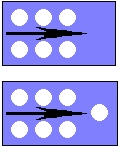
Un motivo è da ricercarsi nel fatto che i numeri erano disposti secondo una disposizione geometrica: i pari formano due file, mentre i dispari hanno sempre una punta. Una freccia allora potrebbe passare agevolmente fra i numeri pari, mentre sarebbe bloccata dai numeri dispari. I numeri pari allora, dando l'idea dell'illimitatezza, erano considerati imperfetti, mentre i numeri dispari, limitati, erano considerati perfetti.

Identificavano qualche attributo umano in molti numeri.

  • l' uno era oggetto di una vera e propria venerazione, in quanto esprimeva l'unità originaria (monade) di cui tutti gli altri numeri, e quindi tutte le cose, erano composti. Esso non era considerato un numero dispari;
  • il due, primo numero pari, esprimeva la contrapposizione al vero sapere, era considerato l'opinione;
  • il quattro esprimeva la giustizia, perché era (escluso sempre l'uno) il primo quadrato perfetto;
  • il cinque era considerato il matrimonio, in quanto unione del primo numero maschile e del primo femminile;
  • il sei era associato al matrimonio ed alla salute perché è il prodotto del primo numero pari e del primo numero dispari; aveva inoltre il significato dell'equilibrio, simboleggiato da due priangoli accoppiati per le basi;
  • il dieci (la sacra tetraktys), era l'unione dei primi quattro numeri (1 + 2 + 3 + 4). Ad essa i Pitagorici rivolgevano questa preghiera:
    «benedici noi, numero divino, tu che hai generato gli dei e gli uomini! Oh santa, santa Tetraktis, tu che contieni la radice e la fonte della creazione sempiterna! Poiché il numero divino inizia con l’unità pura e profonda, e raggiunge in seguito il Quattro sacro; poi genera la madre di tutto, la sacra decade che tutto comprende, il primo - nato, colui che non devia mai, e mai è stanco, il Dieci sacro che detiene la chiave di tutte le cose».

Liberata dal suo misticismo, la filosofia pitagorica conteneva l'idea fondamentale che soltanto attraverso il numero e la forma l'uomo possa afferrare la natura dell'Universo.
La stretta connessione tra forma e numero si trova nella rappresentazione dei numeri in forme geometriche, ad esempio triangoli o quadrati.
Ma non dimentichiamo le loro classificazioni di numeri in amici, perfetti, fortunati...
  [da Dantzig, T, “Il numero - linguaggio della scienza”, La Nuova Italia - Firenze]
 

    SITO LICEO | PAGINA INIZIALE | MAPPA | MITO | LETTERATURA | EPICA | MATEMATICA | SOPRAVVIVENZE| BIBLIOGRAFIA | AUTORI